
某种产品的广告费支出x(单位:百万元)与销售额y(单位:百万元)之间有如下对应数据:
| x | 2 | 4 | 5 | 6 | 8 |
| y | 30 | 40 | 60 | 50 | 70 |
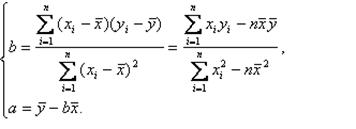
(1)详见解析;(2)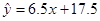
解析试题分析:(1)根据表中所给的五组数据,得到五个点的坐标,在平面直角坐标系中画出散点图.
科目:高中数学
来源:
题型:解答题
某化肥厂甲、乙两个车间包装肥料,在自动包装传送带上每隔30 min抽取一包产品,称其重量,分别记录抽查数据如下:
科目:高中数学
来源:
题型:解答题
小区统计部门随机抽查了区内
科目:高中数学
来源:
题型:解答题
某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,且质量指标值大于或等于102的产品为优质品,现用两种新配方(分别称为A配方和B配方)做试验,各生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
科目:高中数学
来源:
题型:解答题
某市规定,高中学生三年在校期间参加不少于
科目:高中数学
来源:
题型:解答题
“根据《中华人民共和国道路交通安全法》规定:车辆驾驶员血液酒精浓度在20~80 mg/100ml(不含80)之间,属于酒后驾车,血液酒精浓度在80mg/100ml(含80)以上时,属醉酒驾车.”某市交警在该市一交通岗前设点对过往的车辆进行抽查,经过一晚的抽查,共查出酒后驾车者60名,图甲是用酒精测试仪对这60 名酒后驾车者血液中酒精浓度进行检测后依所得结果画出的频率分布直方图.
科目:高中数学
来源:
题型:解答题
通过随机询问110名不同的大学生是否爱好某项运动,得到如下的列联表:
科目:高中数学
来源:
题型:解答题
在某批次的某种灯泡中,随机地抽取
科目:高中数学
来源:
题型:解答题
某兴趣小组欲研究昼夜温差大小与患感冒人数多少之间的关系,他们分别到气象局与某医院抄录了1至6月份每月10号的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
(2)先求出横标和纵标的平均数,得到这组数据的样本中心点,利用最小二乘法求出线性回归方程的系数,代入样本中心点求出a的值,写出线性回归方程.
试题解析:解 (1)散点图如图所示: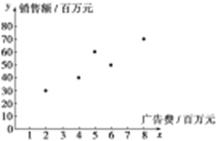
(2)列出下表,并用科学计算器进行有关计算.i 1 2 3 4 5 xi(百万元) 2 4 5 6 8 yi(百万元) 30 40 60 50 70 xiyi 60 160 300 300 560  =5;
=5;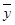 =50;
=50; 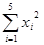 =145;
=145;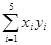 =1 380
=1 380

1加1阅读好卷系列答案
专项复习训练系列答案
初中语文教与学阅读系列答案

完形填空与阅读理解周秘计划系列答案
英语阅读理解150篇系列答案
奔腾英语系列答案
标准阅读系列答案
53English系列答案
考纲强化阅读系列答案
甲:102,101,99,98,103,98,99;
乙:110,115,90,85,75,115,110.
(1)这种抽样方法是哪一种?
(2)将这两组数据用茎叶图表示;
(3)将两组数据比较,说明哪个车间的产品较稳定.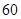 名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过
名网友4月1日这天的网购情况,得到如下数据统计表(图(1)).网购金额超过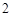 千元的顾客被定义为“网购红人”,网购金额不超过
千元的顾客被定义为“网购红人”,网购金额不超过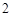 千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为
千元的顾客被定义为“非网购红人”.已知“非网购红人”与“网购红人”人数比恰为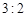 .
.
(1)确定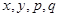 的值,并补全频率分布直方图(图(2)).
的值,并补全频率分布直方图(图(2)).
(2)为进一步了解这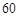 名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定
名网友的购物体验,从“非网购红人”和“网购红人”中用分层抽样的方法确定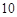 人,若需从这
人,若需从这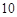 人中随机选取
人中随机选取 人进行问卷调查,设
人进行问卷调查,设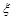 为选取的
为选取的 人中“网购红人”的人数,求
人中“网购红人”的人数,求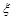 的分布列和数学期望.
的分布列和数学期望.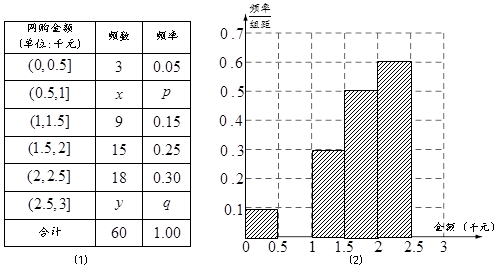
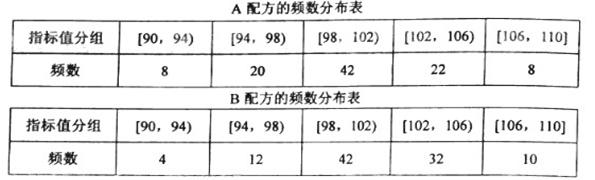
(1)分别估计用A配方,B配方生产的产品的优质品率;
(2)已知用B配方生成的一件产品的利润y(单位:元)与其质量指标值t的关系式为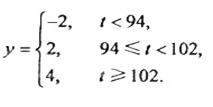
从用B配方生产的产品中任取一件,其利润记为X(单位:元),求X的分布列及数学期望.(以试验结果中质量指标值落入各组的频率作为一件产品的质量指标值落入相应组的概率) 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段 ,
, ,
, ,
, ,
, (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
(Ⅰ)求抽取的200位学生中,参加社区服务时间不少于90小时的学生人数,并估计
从全市高中学生中任意选取一人,其参加社区服务时间不少于90小时的概率;
(Ⅱ)从全市高中学生(人数很多)中任意选取3位学生,记 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量 的分布列和数学期望
的分布列和数学期望 .
.
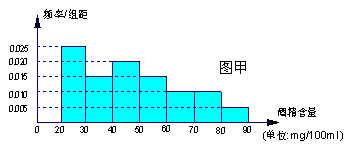
(1)统计方法中,同一组数据常用该组区间的中点值作为代表,图乙的程序框图是对这60名酒后驾车者血液的酒精浓度做进一步的统计,求出图乙输出的S的值,并说明S的统计意义;(图乙中数据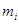 与
与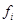 分别表示图甲中各组的组中值及频率)
分别表示图甲中各组的组中值及频率) 
(2)本次行动中,吴、李两位先生都被酒精测试仪测得酒精浓度属于70~90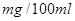 的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90
的范围,但他俩坚称没喝那么多,是测试仪不准,交警大队队长决定在被酒精测试仪测得酒精浓度属于70~90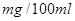 范围的酒后驾车者中随机抽出2人抽血检验,设
范围的酒后驾车者中随机抽出2人抽血检验,设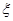 为吴、李两位先生被抽中的人数,求
为吴、李两位先生被抽中的人数,求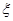 的分布列,并求吴、李两位先生至少有1人被抽中的概率;
的分布列,并求吴、李两位先生至少有1人被抽中的概率;
附:
男
女
总计
爱好
40
20
60
不爱好
20
30
50
总计
60
50
110
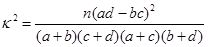
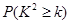
0.050
0.010
0.001

3.841
6.635
10.828
试考查大学生“爱好该项运动是否与性别有关”,若有关,请说明有多少把握。 个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于
个样品,并对其寿命进行追踪调查,将结果列成频率分布表如下.根据寿命将灯泡分成优等品、正品和次品三个等级,其中寿命大于或等于 天的灯泡是优等品,寿命小于
天的灯泡是优等品,寿命小于 天的灯泡是次品,其余的灯泡是正品.
天的灯泡是次品,其余的灯泡是正品.
(1)根据频率分布表中的数据,写出寿命(天) 频数 频率 














合计 

 、
、 的值;
的值;
(2)某人从灯泡样品中随机地购买了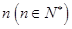 个,如果这
个,如果这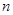 个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求
个灯泡的等级情况恰好与按三个等级分层抽样所得的结果相同,求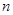 的最小值;
的最小值;
(3)某人从这个批次的灯泡中随机地购买了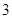 个进行使用,若以上述频率作为概率,用
个进行使用,若以上述频率作为概率,用 表示此人所购买的灯泡中次品的个数,求
表示此人所购买的灯泡中次品的个数,求 的分布列和数学期望.
的分布列和数学期望.
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验.日期 1月
10日2月
10日3月
10日4月
10日5月
10日6月
10日昼夜温差
x(℃)10 11 13 12 8 6 就诊人数
y(个)22 25 29 26 16 12
(1)求选取的2组数据恰好是相邻两个月的概率.
(2)若选取的是1月与6月的两组数据,请根据2至5月份的数据,求出y关于x的线性回归方程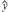 =
= x+
x+ .
.
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式: =
=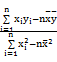 =
=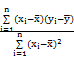 ,
, =
= -
-
 ).
).
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号