
【题目】某市的教育主管部门对所管辖的学校进行年终督导评估,为了解某学校师生对学校教学管理的满意度,分别从教师和不同年级的同学中随机抽取若干师生,进行评分(满分100分),绘制如下频率分布直方图(分组区间为![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ),并将分数从低到高分为四个等级:
),并将分数从低到高分为四个等级:
满意度评分 |
|
|
|
|
满意度等级 | 不满意 | 基本满意 | 满意 | 非常满意 |
已知满意度等级为基本满意的有340人.

(1)求表中![]() 的值及不满意的人数;
的值及不满意的人数;
(2)在等级为不满意的师生中,老师占![]() ,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记
,现从该等级师生中按分层抽样抽取12人了解不满意的原因,并从中抽取3人担任整改督导员,记![]() 为老师整改督导员的人数,求
为老师整改督导员的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.
 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列{an}和等比数列{bn},其中{an}的公差不为0.设Sn是数列{an}的前n项和.若a1 , a2 , a5是数列{bn}的前3项,且S4=16.
(1)求数列{an}和{bn}的通项公式;
(2)若数列{ ![]() }为等差数列,求实数t;
}为等差数列,求实数t;
(3)构造数列a1 , b1 , a2 , b1 , b2 , a3 , b1 , b2 , b3 , …,ak , b1 , b2 , …,bk , …,若该数列前n项和Tn=1821,求n的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在下列结论中: ①函数y=sin(kπ﹣x)(k∈Z)为奇函数;
②函数 ![]() 的图象关于点
的图象关于点 ![]() 对称;
对称;
③函数 ![]() 的图象的一条对称轴为
的图象的一条对称轴为 ![]() π;
π;
④若tan(π﹣x)=2,则cos2x= ![]() .
.
其中正确结论的序号为(把所有正确结论的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗质地均匀的正方体骰子(六个面的点数分别为1,2,3,4,5,6)先后抛掷两次,记第一次出现的点数为x,第二次出现的点数为y.
(1)求事件“x+y≤3”的概率;
(2)求事件“|x﹣y|=2”的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 在区间
在区间![]() 上的最大值和最小值;
上的最大值和最小值;
(2)若在区间![]() 上, 函数
上, 函数![]() 的图象恒在直线
的图象恒在直线![]() 下方, 求
下方, 求![]() 的取值范围;
的取值范围;
(3)设![]() .当
.当![]() 时, 若对于任意
时, 若对于任意![]() ,存在
,存在![]() ,使
,使![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC的周长为l,面积为S,则△ABC的内切圆半径为r= ![]() .将此结论类比到空间,已知四面体ABCD的表面积为S,体积为V,则四面体ABCD的内切球的半径R= .
.将此结论类比到空间,已知四面体ABCD的表面积为S,体积为V,则四面体ABCD的内切球的半径R= .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】椭圆![]() (
(![]() ),原点
),原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,其中:点
,其中:点![]() ,点
,点![]() .
.
(1)求该椭圆![]() 的离心率
的离心率![]() ;
;
(2)经过椭圆右焦点![]() 的直线
的直线![]() 和该椭圆交于
和该椭圆交于![]() 两点,点
两点,点![]() 在椭圆上,
在椭圆上, ![]() 为原点,若
为原点,若![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】两千多年前,古希腊毕达哥拉斯学派的数学家曾经在沙滩上研究数学问题.他们在沙滩上画点或用小石子表示数,按照点或小石子能排列的形状对数进行分类.如下图中实心点的个数5,9,14,20,…为梯形数.根据图形的构成,记此数列的第2013项为a2013 , 则a2013﹣5=( ) 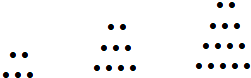
A.2019×2013
B.2019×2012
C.1006×2013
D.2019×1006
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com