
”¾ĢāÄæ”æĪŖĮĖŅżµ¼¾ÓĆńŗĻĄķÓĆĖ®£¬Ä³ŹŠ¾ö¶ØČ«ĆꏵŹ©½×ĢŻĖ®¼Ū£¬½×ĢŻĖ®¼ŪŌŌņÉĻŅŌ×”Õ¬£ØŅ»Ģ××”Õ¬ĪŖŅ»»§£©µÄŌĀÓĆĖ®ĮæĪŖ»ł×¼¶Ø¼Ū£¬¾ßĢå»®·Ö±ź×¼Čē±ķ£ŗ
½×ĢŻ¼¶±š | µŚŅ»½×ĢŻĖ®Įæ | µŚ¶ž½×ĢŻĖ®Įæ | µŚČż½×ĢŻĖ®Įæ |
ŌĀÓĆĖ®Įæ·¶Ī§£Øµ„Ī»£ŗĮ¢·½Ć×£© | £Ø0£¬10] | £Ø10£¬15] | £Ø15£¬+”Ž£© |
“Ó±¾ŹŠĖ껜³éČ”ĮĖ10»§¼ŅĶ„£¬Ķ³¼ĘĮĖĶ¬Ņ»øöŌĀµÄÓĆĖ®Į棬µĆµ½ČēĶ¼ĖłŹ¾µÄ¾„Ņ¶Ķ¼£®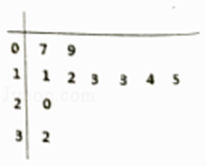
£Ø1£©ĻÖŅŖŌŚÕā10»§¼ŅĶ„ÖŠČĪŅāєȔ3»§£¬ĒóČ”µ½µŚ¶ž½×ĢŻĖ®ĮæµÄ»§ŹżµÄ·Ö²¼ĮŠŗĶ¾łÖµ£»
£Ø2£©ÓĆ³éµ½µÄ10»§¼ŅĶ„×÷ĪŖŃł±¾¹Ą¼ĘČ«ŹŠµÄ¾ÓĆńÓĆĖ®Ēéæö£¬“ÓČ«ŹŠŅĄ“ĪĖ껜³éČ”10»§£¬Čō³éµ½n»§ŌĀÓĆĖ®ĮæĪŖµŚ¶ž½×ĢŻĖ®ĮæµÄæÉÄÜŠŌ×ī“ó£¬Ēó³önµÄÖµ£®
”¾“š°ø”æ
£Ø1£©½ā£ŗÓɾ„Ņ¶Ķ¼æÉÖŖ£ŗ³éČ”µÄ10»§ÖŠÓĆĖ®ĮæĪŖŅ»½×µÄÓŠ2»§£¬¶ž½×µÄÓŠ6»§£¬Čż½×µÄÓŠ2»§£®Č”µ½µŚ¶ž½×ĢŻĖ®ĮæµÄ»§ŹżXµÄȔֵæÉÄÜĪŖ0£¬1£¬2£¬3£®ŌņP£ØX=k£©= ![]() £¬æÉµĆ£ŗP£ØX=0£©=
£¬æÉµĆ£ŗP£ØX=0£©= ![]() £¬P£ØX=1£©=
£¬P£ØX=1£©= ![]() £¬P£ØX=2£©=
£¬P£ØX=2£©= ![]() £¬
£¬
P£ØX=3£©= ![]() £®
£®
æɵĆX·Ö²¼ĮŠĪŖ£ŗ
X | 0 | 1 | 2 | 3 |
P | | | | |
EX=0”Į ![]() +1”Į
+1”Į ![]() +2”Į
+2”Į ![]() +3”Į
+3”Į ![]() =
= ![]()
£Ø2£©½ā£ŗÉč“ÓČ«ŹŠŅĄ“ĪĖ껜³éČ”10»§£¬³éµ½Y»§ŌĀÓĆĖ®ĮæĪŖµŚ¶ž½×ĢŻĖ®Į棬ŌņY”«B ![]() £®
£®
P£ØY=k£©= ![]() £Øk=0£¬1£¬2£¬”£¬10£©£®
£Øk=0£¬1£¬2£¬”£¬10£©£®
Éčt= ![]() =
= ![]() £®
£®
Čōt£¾1£¬Ōņk£¼6.6£¬P£ØY=k©1£©£¼P£ØY=k©1£©£®Čōt£¼1£¬Ōņk£¾6.6£¬P£ØY=k©1£©£¾P£ØY=k©1£©£¬
kČ”6£¬»ņ7µÄæÉÄÜŠŌ±Č½Ļ“ó£®
¾¹żŃéÖ¤k=6Ź±£¬ ![]() =
= ![]() £¾1£®”ąn=6
£¾1£®”ąn=6
”¾½āĪö”放£Ø1£©Óɾ„Ņ¶Ķ¼æÉÖŖ£ŗ³éČ”µÄ10»§ÖŠÓĆĖ®ĮæĪŖŅ»½×µÄÓŠ2»§£¬¶ž½×µÄÓŠ6»§£¬Čż½×µÄÓŠ2»§£®Č”µ½µŚ¶ž½×ĢŻĖ®ĮæµÄ»§ŹżXµÄȔֵæÉÄÜĪŖ0£¬1£¬2£¬3£®ĄūÓĆP£ØX=k£©= ![]() £¬æɵĆXµÄøÅĀŹ·Ö²¼ĮŠ¼°Ę䏿ѧʌĶū£®£Ø2£©Éč“ÓČ«ŹŠŅĄ“ĪĖ껜³éČ”10»§£¬³éµ½Y»§ŌĀÓĆĖ®ĮæĪŖµŚ¶ž½×ĢŻĖ®Į棬ŌņY”«B
£¬æɵĆXµÄøÅĀŹ·Ö²¼ĮŠ¼°Ę䏿ѧʌĶū£®£Ø2£©Éč“ÓČ«ŹŠŅĄ“ĪĖ껜³éČ”10»§£¬³éµ½Y»§ŌĀÓĆĖ®ĮæĪŖµŚ¶ž½×ĢŻĖ®Į棬ŌņY”«B ![]() £®P£ØY=k£©=
£®P£ØY=k£©= ![]() £Øk=0£¬1£¬2£¬”£¬10£©£®Éčt=
£Øk=0£¬1£¬2£¬”£¬10£©£®Éčt= ![]() =
= ![]() £®ÓÉt£¾1£¬æɵĆk£¼6.6£¬P£ØY=k©1£©£¼P£ØY=k©1£©£®ÓÉt£¼1£¬Ōņk£¾6.6£¬P£ØY=k©1£©£¾P£ØY=k©1£©£¬¼“æÉµĆ³ö£®
£®ÓÉt£¾1£¬æɵĆk£¼6.6£¬P£ØY=k©1£©£¼P£ØY=k©1£©£®ÓÉt£¼1£¬Ōņk£¾6.6£¬P£ØY=k©1£©£¾P£ØY=k©1£©£¬¼“æÉµĆ³ö£®
”¾æ¼µć¾«Īö”æ±¾ĢāÖ÷ŅŖæ¼²éĮĖ¾„Ņ¶Ķ¼ŗĶĄėÉ¢ŠĶĖ껜±äĮæ¼°Ęä·Ö²¼ĮŠµÄĻą¹ŲÖŖŹ¶µć£¬ŠčŅŖÕĘĪÕ¾„Ņ¶Ķ¼ÓÖ³Ę”°Ö¦Ņ¶Ķ¼”±£¬ĖüµÄĖ¼Ā·ŹĒ½«Źż×éÖŠµÄŹż°“Ī»Źż½ųŠŠ±Č½Ļ£¬½«ŹżµÄ“óŠ”»ł±¾²»±ä»ņ±ä»Æ²»“óµÄĪ»×÷ĪŖŅ»øöÖ÷øɣؾ„£©£¬½«±ä»Æ“óµÄĪ»µÄŹż×÷ĪŖ·ÖÖ¦£ØŅ¶£©£¬ĮŠŌŚÖ÷øɵÄŗóĆę£¬ÕāŃł¾ĶæÉŅŌĒ峞µŲ擵½ĆæøöÖ÷øÉŗóĆęµÄ¼øøöŹż£¬ĆæøöŹż¾ßĢåŹĒ¶ąÉŁ£»ŌŚÉä»÷”¢²śĘ·¼ģŃéµČĄż×ÓÖŠ£¬¶ŌÓŚĖ껜±äĮæXæÉÄÜČ”µÄÖµ£¬ĪŅĆĒæÉŅŌ°“Ņ»¶Ø“ĪŠņŅ»Ņ»ĮŠ³ö£¬ÕāŃłµÄĖ껜±äĮ潊×öĄėÉ¢ŠĶĖ껜±äĮ森ĄėÉ¢ŠĶĖ껜±äĮæµÄ·Ö²¼ĮŠ£ŗŅ»°ćµÄ,ÉčĄėÉ¢ŠĶĖ껜±äĮæXæÉÄÜČ”µÄÖµĪŖx1,x2,.....,xi,......,xn£¬XČ”ĆæŅ»øöÖµ xi(i=1,2,......£©µÄøÅĀŹP(¦Ī=xi£©£½Pi£¬Ōņ³Ę±ķĪŖĄėÉ¢ŠĶĖ껜±äĮæX µÄøÅĀŹ·Ö²¼£¬¼ņ³Ę·Ö²¼ĮŠ²ÅÄÜÕżČ·½ā“š“ĖĢā£®


 ŌĶĮæģ³µĻµĮŠ“š°ø
ŌĶĮæģ³µĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚĖÄĄā׶ ![]() ÖŠ£¬
ÖŠ£¬ ![]() £¬ĒŅ
£¬ĒŅ ![]() .
.
£Ø1£©Ö¤Ć÷£ŗĘ½Ćę ![]() ”ĶĘ½Ćę
”ĶĘ½Ćę ![]() £»
£»
£Ø2£©Čō ![]() £¬
£¬ ![]() £¬Ēó¶žĆę½Ē
£¬Ēó¶žĆę½Ē ![]() µÄÓąĻŅÖµ.
µÄÓąĻŅÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖČ«¼ÆU=R£¬¼ÆŗĻA={x|x2©x©6”Ü0}£¬ ![]() £¬ÄĒĆ“¼ÆŗĻA”É£ØUB£©=£Ø £©
£¬ÄĒĆ“¼ÆŗĻA”É£ØUB£©=£Ø £©
A.[©2£¬4£©
B.£Ø©1£¬3]
C.[©2£¬©1]
D.[©1£¬3]
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖÄĄā׶ ![]() µÄµ×Ćę
µÄµ×Ćę ![]() ŹĒ¾ŲŠĪ£¬Ę½Ćę
ŹĒ¾ŲŠĪ£¬Ę½Ćę ![]() Ę½Ćę
Ę½Ćę ![]() £¬
£¬ ![]() ŹĒ
ŹĒ ![]() µÄÖŠµć£¬ĒŅ
µÄÖŠµć£¬ĒŅ ![]() ,
, ![]() .
.
£Ø¢ń£©ĒóÖ¤£ŗ ![]() Ę½Ćę
Ę½Ćę ![]() £»
£»
£Ø¢ņ£© ĒóČżĄā׶ ![]() µÄĢå»ż.
µÄĢå»ż.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ”°÷ČĮ¦ŗģ¹ČĢ²”±²ÅŅÕÕ¹Ź¾ĘĄ±ČÖŠ£¬²ĪČüŃ”ŹÖ³É¼ØµÄ¾„Ņ¶Ķ¼ŗĶʵĀŹ·Ö²¼Ö±·½Ķ¼¶¼ŹÜµ½²»Ķ¬³Ģ¶ČµÄĖš»µ£¬æɼū²æ·ÖČēĶ¼ĖłŹ¾£®
£Ø1£©øł¾ŻĶ¼ÖŠŠÅĻ¢£¬½«Ķ¼ŅŅÖŠµÄʵĀŹ·Ö²¼Ö±·½Ķ¼²¹³äĶźÕū£»
£Ø2£©øł¾ŻĘµĀŹ·Ö²¼Ö±·½Ķ¼¹Ą¼ĘŃ”ŹÖ³É¼ØµÄĘ½¾łÖµ£ØĶ¬Ņ»×鏿¾ŻÓĆøĆĒų¼äµÄÖŠµćÖµ×÷“ś±ķ£©£»
£Ø3£©“ӳɼØŌŚ[80£¬100]µÄŃ”ŹÖÖŠČĪŃ”2ČĖ½ųŠŠPK£¬ĒóÖĮÉŁÓŠ1 ČĖ³É¼ØŌŚ[90£¬100]µÄøÅĀŹ£®


²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖŹżĮŠ![]() Āś×ć£ŗ
Āś×ć£ŗ![]()
(1) Ö¤Ć÷£ŗŹżĮŠ![]() ŹĒµČ±ČŹżĮŠ£»
ŹĒµČ±ČŹżĮŠ£»
(2) ĒóŹ¹²»µČŹ½![]() ³ÉĮ¢µÄĖłÓŠÕżÕūŹżm”¢nµÄÖµ£»
³ÉĮ¢µÄĖłÓŠÕżÕūŹżm”¢nµÄÖµ£»
(3) Čē¹ū³£Źż0 < t < 3£¬¶ŌÓŚČĪŅāµÄÕżÕūŹżk£¬¶¼ÓŠ![]() ³ÉĮ¢£¬ĒótµÄȔֵ·¶Ī§£®
³ÉĮ¢£¬ĒótµÄȔֵ·¶Ī§£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚÖ±½ĒĢŻŠĪABCDÖŠ£¬AB”ĶAD£¬AB”ĪDC£¬AB=2£¬AD=DC=1£¬Ķ¼ÖŠŌ²»”ĖłŌŚŌ²µÄŌ²ŠÄĪŖµćC£¬°ė¾¶ĪŖ ![]() £¬ĒŅµćPŌŚĶ¼ÖŠŅõÓ°²æ·Ö£Ø°üĄØ±ß½ē£©ŌĖ¶Æ£®Čō
£¬ĒŅµćPŌŚĶ¼ÖŠŅõÓ°²æ·Ö£Ø°üĄØ±ß½ē£©ŌĖ¶Æ£®Čō ![]() =x
=x ![]() +y
+y ![]() £¬ĘäÖŠx£¬y”ŹR£¬Ōņ4x©yµÄȔֵ·¶Ī§ŹĒ£Ø £©
£¬ĘäÖŠx£¬y”ŹR£¬Ōņ4x©yµÄȔֵ·¶Ī§ŹĒ£Ø £© 
A.![]()
B.![]()
C.![]()
D.![]()
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ¶Æµć ![]() µ½µć
µ½µć ![]() µÄ¾ąĄė±ČĖüµ½Ö±Ļß
µÄ¾ąĄė±ČĖüµ½Ö±Ļß ![]() µÄ¾ąĄėŠ”
µÄ¾ąĄėŠ” ![]() £¬¼Ē¶Æµć
£¬¼Ē¶Æµć ![]() µÄ¹ģ¼£ĪŖ
µÄ¹ģ¼£ĪŖ ![]() .ČōŅŌ
.ČōŅŌ ![]() ĪŖŌ²ŠÄ£¬
ĪŖŌ²ŠÄ£¬ ![]() ĪŖ°ė¾¶£Ø
ĪŖ°ė¾¶£Ø ![]() £©×÷Ō²£¬·Ö±š½»
£©×÷Ō²£¬·Ö±š½» ![]() ÖįÓŚ
ÖįÓŚ ![]() Į½µć£¬Į¬½į²¢ŃÓ³¤
Į½µć£¬Į¬½į²¢ŃÓ³¤ ![]() £¬·Ö±š½»ĒśĻß
£¬·Ö±š½»ĒśĻß ![]() ÓŚ
ÓŚ ![]() Į½µć.
Į½µć.
£Ø1£©ĒóĒśĻß ![]() µÄ·½³Ģ£»
µÄ·½³Ģ£»
£Ø2£©ĒóÖ¤£ŗÖ±Ļß ![]() µÄŠ±ĀŹĪŖ¶ØÖµ.
µÄŠ±ĀŹĪŖ¶ØÖµ.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗøßÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æµć![]() µ½Ö±Ļß
µ½Ö±Ļß![]() µÄ¾ąĄėµČÓŚ4£¬ĒŅŌŚ²»µČŹ½
µÄ¾ąĄėµČÓŚ4£¬ĒŅŌŚ²»µČŹ½![]() ±ķŹ¾µÄĘ½ĆęĒųÓņÄŚ£¬Ōņµć
±ķŹ¾µÄĘ½ĆęĒųÓņÄŚ£¬Ōņµć![]() µÄ×ų±źŹĒ____£®
µÄ×ų±źŹĒ____£®
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com