
【题目】在如图所示的五面体![]() 中,四边形
中,四边形![]() 为菱形,且
为菱形,且![]() ,
, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.
中点.
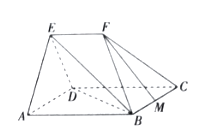
(1)求证: ![]() 平面
平面![]() ;
;
(2)若平面![]() 平面
平面![]() ,求
,求![]() 到平面
到平面![]() 的距离.
的距离.
【答案】(1)见解析;(2)![]()
【解析】试题分析:
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,由线面平行的判定定理可得
,由线面平行的判定定理可得![]() 平面
平面![]() ;再由
;再由![]() 平面
平面![]() 可得
可得![]() ;由题意可证得四边形
;由题意可证得四边形![]() 为平行四边形,故得
为平行四边形,故得![]() ,从而得到
,从而得到![]() 平面
平面![]() ,由面面平行的判定可得平面
,由面面平行的判定可得平面![]() 平面
平面![]() ,由此可得结论成立.(2)由(1)得
,由此可得结论成立.(2)由(1)得![]() 平面
平面![]() ,故
,故![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离.取
的距离.取![]() 的中点
的中点![]() ,连接
,连接![]() ,可证得
,可证得![]() ,
, ![]() ,从而可得
,从而可得![]() 平面
平面![]() ,在此基础上可得
,在此基础上可得![]() ,
, ![]() .然后设
.然后设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,由
,由![]() 可得所求.
可得所求.
试题解析:
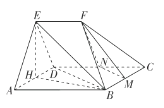
(1)取![]() 中点
中点![]() ,连接
,连接![]() ,
,
因为![]() 分别为
分别为![]() 中点,所以
中点,所以![]() ,
,
又![]() 平面
平面![]() ,且
,且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() .
.
又![]() ,
, ![]() ,
,
所以![]() ,
, ![]() .
.
所以四边形![]() 为平行四边形.
为平行四边形.
所以![]() .
.
又![]() 平面
平面![]() 且
且![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ,
,
又![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() .
.
(2)由(1)得![]() 平面
平面![]() ,所以
,所以![]() 到平面
到平面![]() 的距离等于
的距离等于![]() 到平面
到平面![]() 的距离.
的距离.
取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
因为四边形![]() 为菱形,且
为菱形,且![]() ,
, ![]() ,
,
所以![]() ,
, ![]() ,
,
因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,
, ![]() ,
,
因为![]() ,所以
,所以![]() ,
,
所以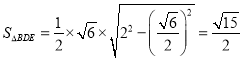 ,
,
设![]() 到平面
到平面![]() 的距离为
的距离为![]() ,又因为
,又因为![]() ,
,
所以由![]() ,得
,得![]() ,
,
解得![]() .
.
即![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知下列说法:
①命题“x0∈R,x+1>3x0”的否定是“x∈R,x2+1<3x”;
②已知p,q为两个命题,若“p∨q”为假命题,则“¬p∧¬q”为真命题
③“a>2”是“a>5”的充分不必要条件
④“若xy=0,则x=0且y=0”的逆否命题为真命题
其中正确说法的个数为( )
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=b·ax(其中a,b为常量,且a>0,a≠1)的图象经过点A(1,6),B(3,24).
(1)求f(x);
(2)若不等式(![]() )x+(
)x+(![]() )x-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
)x-m≥0在x∈(-∞,1]时恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数![]() 和二次函数
和二次函数![]() 满足:
满足:![]() ,
,![]() ,
,![]()
(1)求![]() 和
和![]() 的解析式;
的解析式;
(2)若对于![]() ,
,![]() ,均有
,均有![]() 成立,求a的取值范围;
成立,求a的取值范围;
(3)设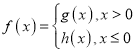 ,在(2)的条件下,讨论方程
,在(2)的条件下,讨论方程![]() 的解的个数.
的解的个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com