
【题目】如图,在多面体![]() 中,平面
中,平面![]() 平面
平面![]() ,四边形
,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 是等腰直角三角形,且
是等腰直角三角形,且![]() ,
,![]() 平面
平面![]() ,
,![]() .
.

(1)求异面直线![]() 和
和![]() 所成角的余弦值;
所成角的余弦值;
(2)求二面角![]() 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
【题目】【选修4-4:坐标系与参数方程】
在平面直角坐标系![]() ,已知曲线
,已知曲线 (
(![]() 为参数),在以
为参数),在以![]() 原点为极点,
原点为极点, ![]() 轴的非负半轴为极轴建立的极坐标系中,直线
轴的非负半轴为极轴建立的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() 。
。
(1)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)过点![]() 且与直线
且与直线![]() 平行的直线
平行的直线![]() 交
交![]() 于
于![]() ,
, ![]() 两点,求点
两点,求点![]() 到
到![]() ,
, ![]() 的距离之积。
的距离之积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2010年至2018年之间,受益于基础设施建设对光纤产品的需求,以及个人计算机及智能手机的下一代规格升级,电动汽车及物联网等新机遇,全球连接器行业增长呈现加速状态.根据如下折线图,下列结论正确的个数为( )
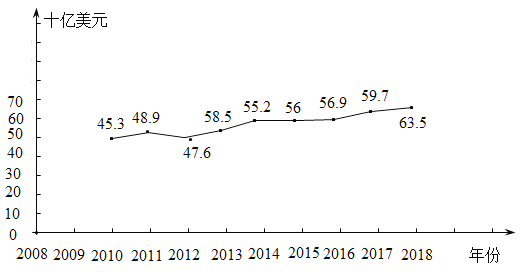
①每年市场规模逐年增加;
②市场规模增长最快的是2013年至2014年;
③这8年的市场规模增长率约为40%;
④2014年至2018年每年的市场规模相对于2010年至2014年每年的市场规模,数据方差更小,变化比较平稳.
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(1)当![]() 时,
时,
①若曲线![]() 与直线
与直线![]() 相切,求c的值;
相切,求c的值;
②若曲线![]() 与直线
与直线![]() 有公共点,求c的取值范围.
有公共点,求c的取值范围.
(2)当![]() 时,不等式
时,不等式![]() 对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
对于任意正实数x恒成立,当c取得最大值时,求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关……”其大意为:“某人从距离关口三百七十八里处出发,第一天走得轻快有力,从第二天起,由于脚痛,每天走的路程为前一天的一半,共走了六天到达关口……” 那么该人第一天走的路程为______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥P-ABC的平面展开图中,四边形ABCD为边长等于![]() 的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:
的正方形,△ABE和△BCF均为正三角形,在三棱锥P-ABC中:

(1)证明:平面PAC⊥平面ABC;
(2)若点M为棱PA上一点且![]() ,求二面角P-BC-M的余弦值.
,求二面角P-BC-M的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了贯彻落实党中央对新冠肺炎疫情防控工作的部署和要求,坚决防范疫情向校园蔓延,切实保障广大师生身体健康和生命的安全,教育主管部门决定通过电视频道、网络平台等多种方式实施线上教育教学工作.某教育机构为了了解人们对其数学网课授课方式的满意度,从经济不发达的A城市和经济发达的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如下:
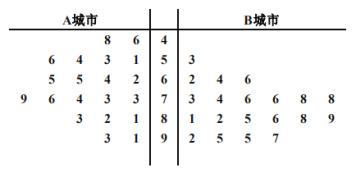
若评分不低于80分,则认为该用户对此教育机构授课方式“认可”,否则认为该用户对此教育机构授课方式“不认可”.
(1)请根据此样本完成下列2×2列联表,并据此列联表分析,能否有95%的把握认为城市经济状况与该市的用户认可该教育机构授课方式有关?
认可 | 不认可 | 合计 | |
A城市 | |||
B城市 | |||
合计 |
(2)以该样本中A,B城市的用户对此教育机构授课方式“认可”的频率分别作为A,B城市用户对此教育机构授课方式“认可”的概率.现从A城市和B城市的所有用户中分别随机抽取2个用户,用X表示这4个用户中对此教育机构授课方式“认可”的用户个数,求X的分布列.
参考公式: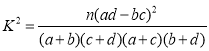 ,其中
,其中![]() .
.
参考数据:
| 0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com