解:(I)因为
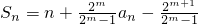
①
所以
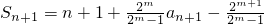
②(2分)
由②-①,得
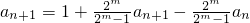
化简得,
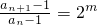
,(6分)
又n=1时,a
1=2
m+1,(7分)
所以{a
n-1}是以a
1=2
m+1为首项,2
m为公比的等比数列.(8分)
(II)由(I)得a
n=2
mn+1,(9分)
因为b
n=3n+1-a
n=3n-2
mn,
所以b
n+1=3(n+1)-2
m(n+1),
因此b
n+1-b
n=3-2
mn(2
m-1),(11分)
因为m≥2,所以2
m-1≥3,2
mn>1,
所以b
n+1-b
n<0,即b
n+1<b
n对n∈N
*恒成立,
所以f(m)=b
1=3-2
m,(14分)
从而f(m)
max=3-4=-1.(16分)
(若设f(x)=3x-(2
m)
x,利用导数求该函数为减函数同样得满分.)
分析:(I)利用已知所给的递推公式及a
n+1=S
n+1-S
n可得得
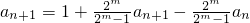
,整理可得,
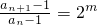
及a
1=2
m+1,可证
(II))由(I)得a
n=2
mn+1由b
n=3n+1-a
n=3n-2
mn,可得b
n+1=3(n+1)-2
m(n+1),从而可得b
n+1-b
n=3-2
mn(2
m-1)由m≥2,可得2
m-1≥3,2
mn>1,即b
n+1<b
n对n∈N
*恒成立,f(m)=b
1=3-2
m,从而可求f(m)
max点评:(1)利用定义
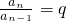
是证明数列为等比数列的常用方法,另外等比数列的等比中项法的应用也要主要掌握.
(2)利用作差法证明数列的单调性进而求解数列的最值问题是解决此题的关键.

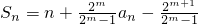 ,其中m是与n无关的常数,且m≠0,n∈N*.
,其中m是与n无关的常数,且m≠0,n∈N*.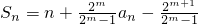 ①
①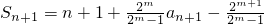 ②(2分)
②(2分)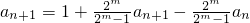
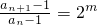 ,(6分)
,(6分)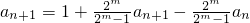 ,整理可得,
,整理可得,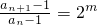 及a1=2m+1,可证
及a1=2m+1,可证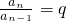 是证明数列为等比数列的常用方法,另外等比数列的等比中项法的应用也要主要掌握.
是证明数列为等比数列的常用方法,另外等比数列的等比中项法的应用也要主要掌握.
