
已知函数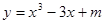 的图像与
的图像与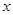 轴恰有两个公共点,则
轴恰有两个公共点,则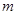 等于( )
等于( )
A.-2或2 B.-9或3 C.-1或1 D.-3或1
A
【解析】
试题分析:求导函数,确定函数的单调性,确定函数的极值点,利用函数y=x3-3x+c的图象与x轴恰有两个公共点,可得极大值等于0或极小值等于0,由此可求m的值解:求导函数可得y′=3(x+1)(x-1),令y′>0,可得x>1或x<-1;令y′<0,可得-1<x<1;,∴函数在(-∞,-1),(1,+∞)上单调增,(-1,1)上单调减,∴函数在x=-1处取得极大值,在x=1处取得极小值,∵函数y=x3-3x+c的图象与x轴恰有两个公共点,∴极大值等于0或极小值等于0,∴1-3+c=0或-1+3+c=0,∴m=-2或2,故选A.
考点:导数的运用
点评:本题考查导数知识的运用,考查函数的单调性与极值,解题的关键是利用极大值等于0或极小值等于0.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源:2014届海南琼海嘉积中学高二上教学监测(三)理科数学试卷(解析版) 题型:选择题
已知函数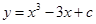 的图像与
的图像与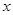 轴恰有两个公共点,则
轴恰有两个公共点,则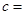
A.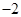 或2 B.
或2 B.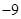 或3 C.
或3 C.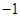 或1 D.
或1 D.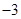 或1
或1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com