
分析 如图所示.把x=c代入椭圆方程可得:$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,解得M$(c,\frac{{b}^{2}}{a})$.过点M作MD⊥y轴,垂足为D.由于△PQM是锐角三角形,可得∠QMD=∠PMD$<\frac{π}{4}$.因此cos∠QMD=$\frac{|MD|}{|QM|}$=$\frac{c}{\frac{{b}^{2}}{a}}$>$cos\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,化简整理即可得出.
解答 解:如图所示.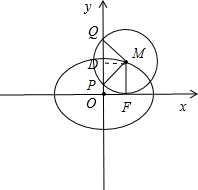
把x=c代入椭圆方程可得:$\frac{{c}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$,解得y=$\frac{{b}^{2}}{a}$.
∴M$(c,\frac{{b}^{2}}{a})$.
过点M作MD⊥y轴,垂足为D.
∵△PQM是锐角三角形,
∴∠QMD=∠PMD$<\frac{π}{4}$,$c<\frac{{b}^{2}}{a}$.
∴cos∠QMD=$\frac{|MD|}{|QM|}$=$\frac{c}{\frac{{b}^{2}}{a}}$>$cos\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,ac<a2-c2,
化为$\sqrt{2}ac>{a}^{2}-{c}^{2}$,ac<a2-c2
∴${e}^{2}+\sqrt{2}e-1$>0,e2+e-1<0.
解得e>$\frac{\sqrt{6}-\sqrt{2}}{2}$,$e<\frac{\sqrt{5}-1}{2}$.
∴该椭圆离心率的取值范围是($\frac{\sqrt{6}-\sqrt{2}}{2}$,$\frac{\sqrt{5}-1}{2}$).
故答案为:($\frac{\sqrt{6}-\sqrt{2}}{2}$,$\frac{\sqrt{5}-1}{2}$).
点评 本题考查了椭圆的标准方程及其性质、圆的性质、锐角三角形的性质、三角函数的单调性,考查了推理能力与计算能力,属于中档题.


 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{5}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=1.
如图,在长方体ABCD-A1B1C1D1中,AB=2,AD=1,AA1=1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com