
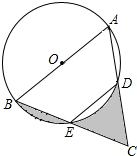
 如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )
如图,AB是⊙O的直径,点E为BC的中点,AB=4,∠BED=120°,则图中阴影部分的面积之和为( )| A. | $\sqrt{3}$ | B. | 2$\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | 1 |
分析 先证明△ABC是等边三角形,从而得到△EDC是等边三角形,边长为2,而$\widehat{BE}$和弦BE围成的部分的面积=$\widehat{DE}$和弦DE所围成的部分的面积,由此能求出图中阴影部分的面积之和.
解答  解:连结AE、OD、OE,
解:连结AE、OD、OE,
∵AB是直径,∴∠AEB=90°,
又∵∠BED=120°,∴∠AED=30°,
∴∠AOD=2∠AED=60°,
∵OA=OD,∴△AOD是等边三角形,
∴∠OAD=60°,
∵点E为BC的中点,∠AEB=90°,
∴AB=AC,
∴△ABC是等边三角形,边长是4,△EDC是等边三角形,边长是2,
∴∠BOE=∠EOD=60°,
∴$\widehat{BE}$和弦BE围成的部分的面积=$\widehat{DE}$和弦DE所围成的部分的面积,
∴阴影部分的面积之和=S△EDC=$\frac{\sqrt{3}}{4}×{2}^{2}=\sqrt{3}$.
故选:A.
点评 本题考查几何图形中阴影部分的面积之和的求法,是中档题,解题时要认真审题,注意圆的性质的合理运用.


科目:高中数学 来源: 题型:选择题
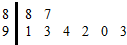 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(x)=\frac{1}{x^2}$ | B. | f(x)=x2+1 | C. | f(x)=x3 | D. | f(x)=|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 16 | C. | 8 | D. | 7 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{3}{2}$,+∞) | B. | (-∞,-$\frac{3}{2}$] | C. | [$\frac{3}{2}$,+∞) | D. | (-∞,$\frac{3}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com