解:(I)由已知可得
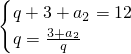
.
解得,q=3或q=-4(舍去),a
2=6
∴a
n=3+(n-1)3=3n
∴b
n=3
n-1(2)证明:∵

∴

∴
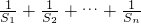
=

=

∵n≥1∴0<

∴

故

.
分析:本题考查的是数列与不等式的综合问题.在解答时:
(1)利用b
2+S
2=12和数列{b
n}的公比
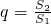
.即可列出方程组求的q、a
2的值,进而获得问题的解答;
(2)首先利用等差数列的前n项和公式计算出数列的前n项和,然后利用放缩法即可获得问题的解答.
点评:本题考查的是数列通项的求法与不等式的综合问题.在解答的过程当中充分体现了解方程的思想、前n项和公式以及放缩法等知识.值得同学们体会反思.

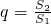 .
.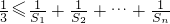 小于
小于 .
.