
【题目】若正项数列![]() 的首项为
的首项为![]() ,且当数列
,且当数列![]() 是公比为
是公比为![]() 的等比数列时,则称数列
的等比数列时,则称数列![]() 为“
为“![]() 数列”.
数列”.
(1)已知数列![]() 的通项公式为
的通项公式为![]() ,证明:数列
,证明:数列![]() 为“
为“![]() 数列”;
数列”;
(2)若数列![]() 为“
为“![]() 数列”,且对任意
数列”,且对任意![]() ,
,![]() 、
、![]() 、
、![]() 成等差数列,公差为
成等差数列,公差为![]() .
.
①求![]() 与
与![]() 间的关系;
间的关系;
②若数列![]() 为递增数列,求
为递增数列,求![]() 的取值范围.
的取值范围.
 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:高中数学 来源: 题型:
【题目】2019年9月25日.阿里巴巴在杭州云栖大会上正式对外发布了含光800AI芯片,在业界标准的ResNet -50测试中,含光800推理性能达到78563lPS,比目前业界最好的AI芯片性能高4倍;能效比500 IPS/W,是第二名的3.3倍.在国内集成电路产业发展中,集成电路设计产业始终是国内集成电路产业中最具发展活力的领域,增长也最为迅速.如图是2014-2018年中国集成电路设计产业的销售额(亿元)及其增速(%)的统计图,则下面结论中正确的是( )
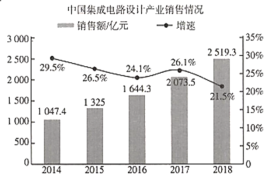
A.2014-2018年,中国集成电路设计产业的销售额逐年增加
B.2014-2017年,中国集成电路设计产业的销售额增速逐年下降
C.2018年中国集成电路设计产业的销售额的增长率比2015年的高
D.2018年与2014年相比,中国集成电路设计产业销售额的增长率约为110%
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知长方形ABCD中,AB=1,∠ABD=60°,现将长方形ABCD沿着对角线BD折起,使平面ABD⊥平面BCD,则折后几何图形的外接球表面积为_____.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() 射线
射线![]() 交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
(1)求曲线C的直角坐标方程及直线l的参数方程;
(2)当直线l倾斜角α为何值时, |BP|·|BQ|取最小值, 并求出|BP|·|BQ|最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学举行的“新冠肺炎”防控知识闭卷考试比赛,总分获得一等奖、二等奖、三等奖的代表队人数情况如下表,该校政教处为使颁奖仪式有序进行,气氛活跃,在颁奖过程中穿插抽奖活动,并用分层抽样的方法从三个代表队中共抽取16人在前排就坐,其中一等奖代表队有6人.
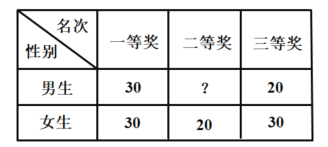
(1)求二等奖代表队的男生人数;
(2)从前排就坐的三等奖代表队员5人(2男3女)中随机抽取3人上台领奖,请求出只有一个男生上台领奖的概率;
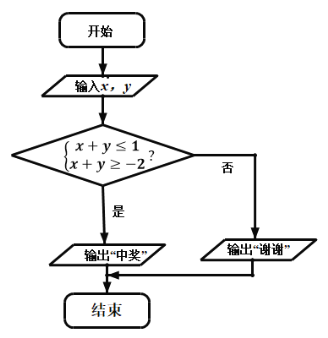
(3)抽奖活动中,代表队员通过操作按键,使电脑自动产生[![]() 2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
2,2]内的两个均匀随机数x,y,随后电脑自动运行如图所示的程序框图的相应程序,若电脑显示“中奖”,则代表队员获相应奖品;若电脑显示“谢谢”,则不中奖,求代表队队员获得奖品的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1,四边形ABCD为等腰梯形,AB=4,AD=DC=CB=2,△ADC沿AC折起,使得平面ADC⊥平面ABC,E为AB的中点,连接DE,DB(如图2).
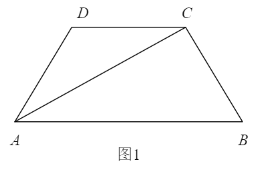
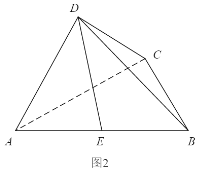
(1)求证:BC⊥AD
(2)求直线DE与平面BCD所成的角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“珠算之父”程大位是我国明代著名的数学家,他的应用巨著《算法统综》中有一首“竹筒容米”问题:“家有九节竹一茎,为因盛米不均平,下头三节四升五,上梢四节三升八,唯有中间两节竹,要将米数次第盛,若有先生能算法,也教算得到天明.”((注)四升五:4.5升,次第盛:盛米容积依次相差同一数量.)用你所学的数学知识求得中间两节竹的容积为
A. 2.2升B. 2.3升
C. 2.4升D. 2.5升
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上的点到准线的最小距离为
上的点到准线的最小距离为![]() .
.
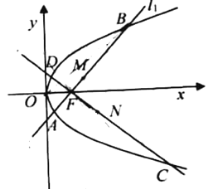
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() 、
、![]() ,
,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点,![]() 分别为弦
分别为弦![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com