
若直线3x+4y-3=0与直线6x+my+14=0平行,则它们之间的距离为 .
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十五第八章第六节练习卷(解析版) 题型:填空题
已知双曲线 -
-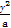 =1的右焦点的坐标为(
=1的右焦点的坐标为(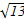 ,0),则该双曲线的渐近线方程为_______.
,0),则该双曲线的渐近线方程为_______.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十三第八章第四节练习卷(解析版) 题型:填空题
若点P在直线l1:x+my+3=0上,过点P的直线l2与圆C:(x-5)2+y2=16只有一个公共点M,且|PM|的最小值为4,则m= .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷(解析版) 题型:填空题
设定点M(-3,4),动点N在圆x2+y2=4上运动,以OM,ON为邻边作平行四边形MONP,则点P的轨迹方程为 .
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十七第八章第八节练习卷(解析版) 题型:选择题
设x1,x2∈R,常数a>0,定义运算“*”:x1*x2=(x1+x2)2-(x1-x2)2,若x≥0,则动点P(x,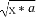 )的轨迹是( )
)的轨迹是( )
(A)圆 (B)椭圆的一部分
(C)双曲线的一部分 (D)抛物线的一部分
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
分别过点A(1,3)和点B(2,4)的直线l1和l2互相平行且有最大距离,则l1的方程是( )
(A)x-y-4=0 (B)x+y-4=0
(C)x=1 (D)y=3
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业五十一第八章第二节练习卷(解析版) 题型:选择题
点P(-1,3)到直线l:y=k(x-2)的距离的最大值等于( )
(A)2 (B)3 (C)3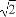 (D)2
(D)2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十四第三章第八节练习卷(解析版) 题型:解答题
在锐角△ABC中,角A,B,C所对的边分别为a,b,c,向量m=(1,cosB),n=(sinB,-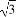 ),且m⊥n.
),且m⊥n.
(1)求角B的大小.
(2)若△ABC的面积为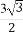 ,a=2,求b的值.
,a=2,求b的值.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学全程总复习课时提升作业二十八第四章第四节练习卷(解析版) 题型:选择题
设△ABC的三个内角为A,B,C,向量m=( sinA,sinB),
sinA,sinB),
n=(cosB, cosA),若m·n=1+cos(A+B),则C=( )
cosA),若m·n=1+cos(A+B),则C=( )
(A) (B)
(B) (C)
(C)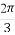 (D)
(D)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com