
(本小题14分)甲和乙参加有奖竞猜闯关活动,活动规则:①闯关过程中,若闯关成功则继续答题;若没通关则被淘汰;②每人最多闯3关;③闯第一关得10万奖金,闯第二关得20万奖金,闯第三关得30万奖金,一关都没过则没有奖金。已知甲每次闯关成功的概率为![]() ,乙每次闯关成功的概率为
,乙每次闯关成功的概率为![]() 。
。
(1)设乙的奖金为![]() ,求
,求![]() 的分布列和数学期望;
的分布列和数学期望;
(2)求甲恰好比乙多30万元奖金的概率.
科目:高中数学 来源:2010年黑龙江省哈六中高三下学期第二次模拟考试数学(理) 题型:解答题
(本小题满分12分)
在清明节前,哈市某单位组织员工参加植树祭扫,林管局在植树前为了保证树苗质量,都会对树苗进行检测,现从甲、乙两种树苗中各抽测了10株树苗的高度,量出它们的高度如下:(单位:厘米)
甲:37 21 31 21 28 19 32 23 25 33
乙:10 30 47 27 46 14 26 11 43 46
(1)根据抽测结果画出茎叶图,并根据你所填写的茎叶图对两种树苗高度作比较,写出3个统计结论;
(2)如果认为甲种树苗高度超过30厘米为优质树苗,那么在己抽测的甲种10株树苗中任选两株栽种,记优质树苗的个数为 ,求
,求 的分布列和期望.
的分布列和期望.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市高三复习必修五综合练习 题型:解答题
(本小题14分)某工厂要制造A种电子装置41台,B种电子装置66台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2㎡,可做A、B的外壳分别为2个和7个,乙种薄钢板每张面积5㎡,可做A、B的外壳分别为7个和9个,求两种薄钢板各用多少张,才能使总的用料面积最小?
查看答案和解析>>
科目:高中数学 来源:2011年广东省招生统一考试理科数学 题型:解答题
(本小题满分13分)
为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生产的产品中分别抽取14件和5件,测量产品中微量元素x,y的含量(单位:毫克).下表是乙厂的5件产品的测量数据:

(1)已知甲厂生产的产品共98件,求乙厂生产的产品数量;
(2)当产品中的微量元素x,y满足≥175且y≥75,该产品为优等品,用上述样本数据估计乙厂生产的优等品的数量;

查看答案和解析>>
科目:高中数学 来源:2010-2011学年广东省中山市高三第一次月考数学理卷 题型:解答题
(本小题满分14分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球。现从甲、乙两个盒内各任取2个球。
(1)求取出的4个球均为黑球的概率;
(2)求取出的4个球中恰有1个红球的概率;
(3)设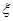 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求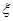 的分布列和数学期望
的分布列和数学期望
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com