
【题目】已知F为抛物线y2=x的焦点,点A,B在该抛物线上且位于x轴的两侧, ![]()
![]() =2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
=2(其中O为坐标原点),则△ABO与△AFO面积之和的最小值是( )
A.2
B.3
C.![]()
D.![]()
【答案】B
【解析】解:设直线AB的方程为:x=ty+m,点A(x1 , y1),B(x2 , y2),
直线AB与x轴的交点为M(m,0),
由 ![]() y2﹣ty﹣m=0,根据韦达定理有y1y2=﹣m,
y2﹣ty﹣m=0,根据韦达定理有y1y2=﹣m,
∵ ![]()
![]() =2,∴x1x2+y1y2=2,
=2,∴x1x2+y1y2=2,
结合 ![]() 及
及 ![]() ,得
,得 ![]() ,
,
∵点A,B位于x轴的两侧,∴y1y2=﹣2,故m=2.
不妨令点A在x轴上方,则y1>0,又 ![]() ,
,
∴S△ABO+S△AFO= ![]() =
= ![]() ×2×(y1﹣y2)+
×2×(y1﹣y2)+ ![]() ×
× ![]() y1 ,
y1 ,
= ![]() .
.
当且仅当 ![]() ,即
,即 ![]() 时,取“=”号,
时,取“=”号,
∴△ABO与△AFO面积之和的最小值是3,故选B.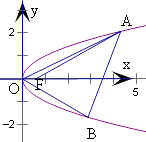
可先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及 ![]()
![]() =2消元,最后将面积之和表示出来,探求最值问题.
=2消元,最后将面积之和表示出来,探求最值问题.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:
【题目】如图,设椭圆 ![]() (a>b>0)的左、右焦点分别为F1 , F2 , 点D在椭圆上.DF1⊥F1F2 ,
(a>b>0)的左、右焦点分别为F1 , F2 , 点D在椭圆上.DF1⊥F1F2 , ![]() =2
=2 ![]() ,△DF1F2的面积为
,△DF1F2的面积为 ![]() .
. 
(1)求椭圆的标准方程;
(2)设圆心在y轴上的圆与椭圆在x轴的上方有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点,求圆的半径.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学为了解在校本科生对参加某项社会实践活动的意向,拟采用分层抽样的方向,从该校四个年级的本科生中抽取一个容量为300的样本进行调查,已知该校一年级、二年级、三年级、四年级的本科生人数之比为4:5:5:6,则应从一年级本科生中抽取名学生.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,且定义域为
,且定义域为![]() .
.
(1)求关于![]() 的方程
的方程![]() 在
在![]() 上的解;
上的解;
(2)若![]() 在区间
在区间![]() 上单调减函数,求实数
上单调减函数,求实数![]() 的取值范围;
的取值范围;
(3)若关于![]() 的方程
的方程![]() 在
在![]() 上有两个不同的实根,求实数
上有两个不同的实根,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=ln(1+x)﹣ln(1﹣x),x∈(﹣1,1).现有下列命题:
①f(﹣x)=﹣f(x);
②f( ![]() )=2f(x)
)=2f(x)
③|f(x)|≥2|x|
其中的所有正确命题的序号是( )
A.①②③
B.②③
C.①③
D.①②
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的值;
的值;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)若![]() 是
是![]() 展开式中所有无理项的二项式系数和,数列
展开式中所有无理项的二项式系数和,数列![]() 是各项都大于1的数组成的数列,试用数学归纳法证明:
是各项都大于1的数组成的数列,试用数学归纳法证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设等差数列{an}的公差为d,点(an , bn)在函数f(x)=2x的图象上(n∈N*).
(1)若a1=﹣2,点(a8 , 4b7)在函数f(x)的图象上,求数列{an}的前n项和Sn;
(2)若a1=1,函数f(x)的图象在点(a2 , b2)处的切线在x轴上的截距为2﹣ ![]() ,求数列{
,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论正确的是( )
A. 函数![]() 在区间
在区间![]() 上的图像是连续不断的一条曲线,若
上的图像是连续不断的一条曲线,若![]() ,则函数
,则函数![]() 在区间
在区间![]() 内无零点
内无零点
B. 函数![]() 在区间
在区间![]() 上的图像是连续不断的一条曲线,若
上的图像是连续不断的一条曲线,若![]() ,则函数
,则函数![]() 在区间
在区间![]() 内可能有零点,且零点个数为偶数
内可能有零点,且零点个数为偶数
C. 函数![]() 在区间
在区间![]() 上的图像是连续不断的一条曲线,若
上的图像是连续不断的一条曲线,若![]() ,则函数
,则函数![]() 在区间
在区间![]() 内必有零点,且零点个数为奇数
内必有零点,且零点个数为奇数
D. 函数![]() 在区间
在区间![]() 上的图像是连续不断的一条曲线,若
上的图像是连续不断的一条曲线,若![]() ,则函数
,则函数![]() 在区间
在区间![]() 内必有零点,但是零点个数不确定
内必有零点,但是零点个数不确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com