
【题目】直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点,且
为坐标原点,且![]() .
.
(1)求![]() 与
与![]() 满足的关系;
满足的关系;
(2)求证:点![]() 到直线
到直线![]() 的距离是定值,并求
的距离是定值,并求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,其准线
,其准线![]() :
:![]() 与
与![]() 轴的交点为
轴的交点为![]() ,过点
,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(1)求抛物线![]() 的方程;
的方程;
(2)点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,证明:存在实数
,证明:存在实数![]() ,使得
,使得![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
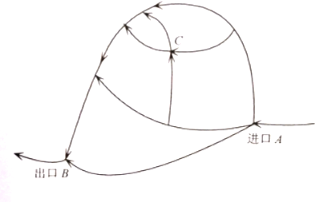
【题目】如图是一旅游景区供游客行走的路线图,假设从进口![]() 开始到出口
开始到出口![]() ,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共
,每遇到一个岔路口,每位游客选择其中一条道路行进是等可能的.现有甲、乙、丙、丁共![]() 名游客结伴到旅游景区游玩,他们从进口
名游客结伴到旅游景区游玩,他们从进口![]() 的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口
的岔路口就开始选择道路自行游玩,并按箭头所指路线行走,最后到出口![]() 集中,设点
集中,设点![]() 是其中的一个交叉路口点.
是其中的一个交叉路口点.
(1)求甲经过点![]() 的概率;
的概率;
(2)设这![]() 名游客中恰有
名游客中恰有![]() 名游客都是经过点
名游客都是经过点![]() ,求随机变量
,求随机变量![]() 的概率分布和数学期望.
的概率分布和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次足球邀请赛共安排了![]() 支球队参加,每支球队预定的比赛场数分别是
支球队参加,每支球队预定的比赛场数分别是![]() ,
,![]() ,…,
,…,![]() .若任两支球队之间至多安排了一场比赛,则称
.若任两支球队之间至多安排了一场比赛,则称![]() 是一个“有效安排”.证明:若
是一个“有效安排”.证明:若![]() 是一个有效安排,且
是一个有效安排,且![]() ,则可去掉一支球队,并重新调整各队之间的对局情况,使
,则可去掉一支球队,并重新调整各队之间的对局情况,使![]() 也是一个有效安排.
也是一个有效安排.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
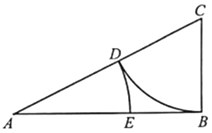
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分形几何学是一门以不规则几何形态为研究对象的几何学.分形的外表结构极为复杂,但其内部却是有规律可寻的.一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.下面我们用分形的方法来得到一系列图形,如图1,线段![]() 的长度为a,在线段
的长度为a,在线段![]() 上取两个点
上取两个点![]() ,
,![]() ,使得
,使得![]() ,以
,以![]() 为一边在线段
为一边在线段![]() 的上方做一个正六边形,然后去掉线段
的上方做一个正六边形,然后去掉线段![]() ,得到图2中的图形;对图2中的最上方的线段
,得到图2中的图形;对图2中的最上方的线段![]() 作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
作相同的操作,得到图3中的图形;依此类推,我们就得到了以下一系列图形:
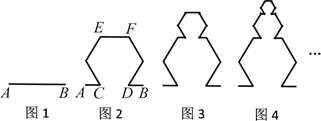
记第![]() 个图形(图1为第1个图形)中的所有线段长的和为
个图形(图1为第1个图形)中的所有线段长的和为![]() ,现给出有关数列
,现给出有关数列![]() 的四个命题:
的四个命题:
①数列![]() 是等比数列;
是等比数列;
②数列![]() 是递增数列;
是递增数列;
③存在最小的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() ;
;
④存在最大的正数![]() ,使得对任意的正整数
,使得对任意的正整数![]() ,都有
,都有![]() .
.
其中真命题的序号是________________(请写出所有真命题的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com