
分析 利用n对0~1之间的均匀随机数x,y,满足$\left\{\begin{array}{l}0<x<1\\ 0<y<1\end{array}\right.$,相应平面区域面积为1,两个数能与1构成钝角三角形三边的数对(x,y),满足$\left\{\begin{array}{l}{x^2}+{y^2}<1\\ x+y>1\end{array}\right.$且$\left\{\begin{array}{l}0<x<1\\ 0<y<1\end{array}\right.$,面积为$\frac{π}{4}-\frac{1}{2}$,结合面积比,即可得出结论.
解答 解:由题意,n对0~1之间的均匀随机数x,y,满足$\left\{\begin{array}{l}0<x<1\\ 0<y<1\end{array}\right.$,相应平面区域面积为1,两个数能与1构成钝角三角形三边的数对(x,y),满足$\left\{\begin{array}{l}{x^2}+{y^2}<1\\ x+y>1\end{array}\right.$且$\left\{\begin{array}{l}0<x<1\\ 0<y<1\end{array}\right.$
面积为$\frac{π}{4}-\frac{1}{2}$,所以$\frac{m}{n}=\frac{π}{4}-\frac{1}{2}$,得π=$\frac{4m}{n}+2$.
故答案为$\frac{4m}{n}+2$.
点评 本题考查了随机模拟法求圆周率的问题,也考查了几何概率的应用问题,是综合题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|0<x<2} | B. | {x|0<x<1} | C. | {x|0≤x<1} | D. | {x|-1<x<0} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 将23(10)化成二进位制数是10111(2) | |
| B. | 在空间坐标系点M(1,2,3)关于x轴的对称点为(1,-2,-3) | |
| C. | 数据:2,4,6,8的方差是数据:1,2,3,4的方差的2倍 | |
| D. | 若点A(-1,0)在圆x2+y2-mx+1=0的外部,则m>-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
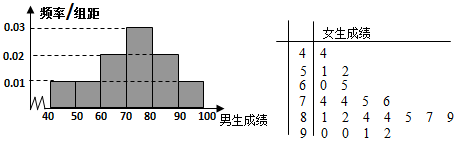
| 优分 | 非优分 | 总计 | |
| 男生 | |||
| 女生 | |||
| 总计 | 50 |
| P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,n⊥β,m⊥n,则α⊥β | B. | 若m∥α,n⊥β,m∥n,则α⊥β | ||
| C. | 若m∥n,m∥α,n∥β,则α∥β | D. | 若m?α,n?α,m∥β,n∥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com