
【题目】如图,PA垂直于以AB为直径的圆所在平面,C为圆上异于A,B的任意一点,![]() 垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒
垂足为E,点F是PB上一点,则下列判断中不正确的是( )﹒

A.![]() 平面PACB.
平面PACB.![]() C.
C.![]() D.平面
D.平面![]() 平面PBC
平面PBC
 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),在以原点为极点,
为参数),在以原点为极点, ![]() 轴正半轴为极轴的极坐标系中,直线
轴正半轴为极轴的极坐标系中,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的普通方程和直线
的普通方程和直线![]() 的倾斜角;
的倾斜角;
(2)设点![]() 和
和![]() 交于
交于![]() 两点,求
两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 是空气质量的一个重要指标,我国
是空气质量的一个重要指标,我国![]() 标准采用世卫组织设定的最宽限值,即
标准采用世卫组织设定的最宽限值,即![]() 日均值在
日均值在![]() 以下空气质量为一级,在
以下空气质量为一级,在![]() 之间空气质量为二级,在
之间空气质量为二级,在![]() 以上空气质量为超标.如图是某地
以上空气质量为超标.如图是某地![]() 月
月![]() 日到
日到![]() 日
日![]() 日均值(单位:
日均值(单位:![]() )的统计数据,则下列叙述不正确的是( )
)的统计数据,则下列叙述不正确的是( )
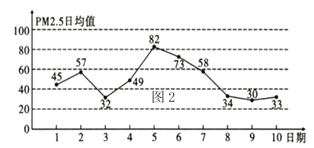
A.从![]() 日到
日到![]() 日,
日,![]() 日均值逐渐降低
日均值逐渐降低
B.这![]() 天的
天的![]() 日均值的中位数是
日均值的中位数是![]()
C.这![]() 天中
天中![]() 日均值的平均数是
日均值的平均数是![]()
D.从这![]() 天的日均
天的日均![]() 监测数据中随机抽出一天的数据,空气质量为一级的概率是
监测数据中随机抽出一天的数据,空气质量为一级的概率是![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三棱锥![]() 的底面
的底面![]() 是等边三角形,点
是等边三角形,点![]() 在平面
在平面![]() 上的射影在
上的射影在![]() 内(不包括边界),
内(不包括边界),![]() .记
.记![]() ,
,![]() 与底面所成角为
与底面所成角为![]() ,
,![]() ;二面角
;二面角![]() ,
,![]() 的平面角为
的平面角为![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,![]() ,
,![]() 之间的大小关系等确定的是()
之间的大小关系等确定的是()
A. ![]() B.
B. ![]()
C. ![]() 是最小角,
是最小角,![]() 是最大角D. 只能确定
是最大角D. 只能确定![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年被称为“新高考元年”,随着上海、浙江两地顺利实施“语数外+3”新高考方案,新一轮的高考改革还将继续在全国推进.辽宁地区也将于2020年开启新高考模式,今年秋季入学的高一新生将面临从物理、化学、生物、政治、历史、地理等6科中任选三科(共20种选法)作为自己将来高考“语数外+3”新高考方案中的“3”.某地区为了顺利迎接新高考改革,在某学校理科班的200名学生中进行了“学生模拟选科数据”调查,每个学生只能从表格中的20种课程组合选择一种学习.模拟选课数据统计如下表:
序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
组合学科 | 物化生 | 物化政 | 物化历 | 物化地 | 物生政 | 物生历 | 物生地 |
人数 | 20人 | 5人 | 10人 | 10人 | 10人 | 15人 | 10人 |
序号 | 8 | 9 | 10 | 11 | 12 | 13 | 14 |
组合学科 | 物政历 | 物政地 | 物历地 | 化生政 | 化生历 | 化生地 | 化政历 |
人数 | 5人 | 0人 | 5人 | …… | 40人 | …… | …… |
序号 | 15 | 16 | 17 | 18 | 19 | 20 | |
组合学科 | 化政地 | 化历地 | 生政历 | 生政地 | 生历地 | 政历地 | 总计 |
人数 | …… | …… | …… | …… | …… | …… | 200人 |
为了解学生成绩与学生模拟选课之间的关系,用分层抽样的方法从这200名学生中抽取40人的样本进行分析。
(1)样本中选择组合6号“物生历”的有多少人?样本中同时选择学习物理和历史的有多少人?
(2)从样本选择学习物理且学习历史的学生中随机抽取3人,求这3人中至少有2人还要学习生物的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将一颗骰子先后抛掷2次,观察向上的点数,事件A:“两数之和为8”,事件B:“两数之和是3的倍数”,事件C:“两个数均为偶数”.
(I)写出该试验的基本事件![]() ,并求事件A发生的概率;
,并求事件A发生的概率;
(II)求事件B发生的概率;
(III)事件A与事件C至少有一个发生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图所示的毕达格拉斯树画是由图(i)利用几何画板或者动态几何画板Geogebra做出来的图片,其中四边形ABCD.AEFG.PQBE都是正方形.如果改变图(i)中![]() 的大小会得到更多不同的“树形”.
的大小会得到更多不同的“树形”.

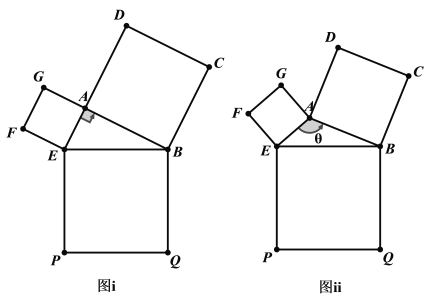
(1)在图(i)中,![]() ,
,![]() ,且
,且![]() ,求AQ;
,求AQ;
(2)在图(ii)中,![]() ,
,![]() ,设
,设![]() ,求AQ的最大值
,求AQ的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,在集合
,在集合![]() 的所有元素个数为2的子集中,把每个子集的较大元素相加和记为a,较小元素之和记为b.
的所有元素个数为2的子集中,把每个子集的较大元素相加和记为a,较小元素之和记为b.
(1)当n=3时,求a, b的值;
(2)当n=4时,求集合![]() 的所有3个元素子集
的所有3个元素子集![]() 中所有元素之和
中所有元素之和![]() ;
;
(3)对任意的![]() ,
,![]() 是否为定值?若是定值,请给出证明并求出这个定值;若不是,请说明理由.
是否为定值?若是定值,请给出证明并求出这个定值;若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com