
(1)求证:![]() ;?
;?
(2)求四面体ABCD的体积;?
(3)若a=5,b=4,c=6,求α的正弦值;?
(4)求AD与平面BCD所成的角〔条件同(3)〕;?
(5)条件同(3),求四面体的外接球半径.
(1)证明:作CE⊥AD交AD于E.?
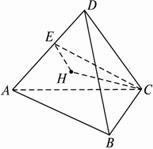
作CH⊥面ABD交ABD于H.?
连结EH,记CH长为h,CE为ha.?
∵CH⊥面ABD,CE⊥AD,?
∴HE⊥AD,sinα=![]() .?
.?
又a·ha·![]() =S,?
=S,?
∴![]() .?
.?
![]() 为常量.同理
为常量.同理![]() ,
,![]() .?
.?
∴![]() .?
.?
(2)解析:过点C作GF∥DB.C为GF中点,连结GD并延长至E.DE=DG.连结EF、AE、AG、AF.
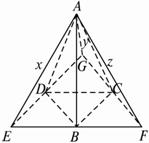
∵AC=![]() GF,∴AG⊥AF.?
GF,∴AG⊥AF.?
同理可得EA⊥FA,AE⊥AG.?
设AE=x,AF=z,AG=y.?
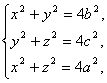
解得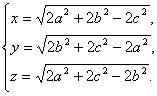
∴VE—AGF?=![]() xyz,?
xyz,?
VA—DBC?=![]() VE—AGF?,?
VE—AGF?,?
VABCD?=![]() .?
.?
(3)解析:V=![]() ?
?
=![]() ×5×3×3
×5×3×3![]() =
=![]() .?
.?
cosθ=![]() .?
.?
∴S=![]() sinθab=
sinθab=![]() ×
×![]() ×5×4=
×5×4=![]() .?
.?
∴d=![]() .∴sinα=
.∴sinα=![]() .?
.?
(4)解析:设所成角为γ.?
sinγ=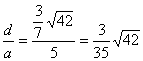 .?
.?
(5)解析:把四面体ABCD补成长方体,设其边长为x、y、z,则有?
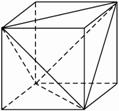
x2+y2=a2, ①?
y2+z2=b2, ②?
z2+x2=c2. ③?
![]() (①+②+③),得(2R)2=a2+b2+c2.?
(①+②+③),得(2R)2=a2+b2+c2.?
∴R=![]() .
.


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,棱长为1的正四面体ABCD中,E、F分别是棱AD、CD的中点,O是点A在平面BCD内的射影.
如图,棱长为1的正四面体ABCD中,E、F分别是棱AD、CD的中点,O是点A在平面BCD内的射影.查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,在四面体ABCD中,平面EFGH分别平行于棱CD、AB,E、F、G、H分别在BD、BC、AC、AD上,且CD=a,AB=b,CD⊥AB.
如图,在四面体ABCD中,平面EFGH分别平行于棱CD、AB,E、F、G、H分别在BD、BC、AC、AD上,且CD=a,AB=b,CD⊥AB.| DE | DB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com