
(本小题满分13分)
袋中有大小相同的三个球,编号分别为1、2和3,从袋中每次取出一个球,若取到的球的编号为偶数,则把该球编号加1(如:取到球的编号为2,改为3)后放回袋中继续取球;若取到球的编号为奇数,则取球停止,用 表示所有被取球的编号之和.
表示所有被取球的编号之和.
(Ⅰ)求 的概率分布;
的概率分布;
(Ⅱ)求 的数学期望与方差.
的数学期望与方差.
科目:高中数学 来源: 题型:解答题
口袋中有大小、质地均相同的7个球,3个红球,4个黑球,现在从中任取3个球。
(1)求取出的球颜色相同的概率;
(2)若取出的红球数设为 ,求随机变量
,求随机变量 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
张师傅驾车从公司开往火车站,途径4个公交站,这四个公交站将公司到火车站
分成5个路段,每个路段的驾车时间都是3分钟,如果遇到红灯要停留1分钟,假设他在各
交通岗是否遇到红灯是相互独立的,并且概率都是
(1)求张师傅此行时间不少于16分钟的概率
(2)记张师傅此行所需时间为Y分钟,求Y的分布列和均值
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球中恰有1个红球的概率;
(Ⅱ)设“从甲盒内取出的2个球恰有1个为黑球”为事件A;“从乙盒内取出的2个球都是黑球”为事件B,求在事件A发生的条件下,事件B发生的概率;
(Ⅲ)设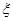 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求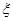 的分布列和数学期望。
的分布列和数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一车间生产A, B, C三种样式的LED节能灯,每种样式均有10W和30W两种型号,某天的产量如右表(单位:个)。按样式分层抽样的方法在这个月生产的灯泡中抽取100个,其中有A样式灯泡25个.
| 型号 | A样式 | B样式 | C样式 |
| 10W | 2000 | z | 3000 |
| 30W | 3000 | 4500 | 5000 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知箱中装有4个白球和5个黑球,且规定:取出一个白球的2分,取出一个黑球的1分.现从该箱中任取(无放回,且每球取到的机会均等)3个球,记随机变量X为取出3球所得分数之和.
(Ⅰ)求X的分布列;
(Ⅱ)求X的数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)某校举行环保知识大奖赛,比赛分初赛和决赛两部分,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3题者直接进入决赛,答错3题者则被淘汰,已知选手甲答题连续两次答错的概率为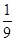 ,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为
,(已知甲回答每个问题的正确率相同,并且相互之间没有影响。)(I)求甲选手回答一个问题的正确率;(Ⅱ)求选手甲可进入决赛的概率;(Ⅲ)设选手甲在初赛中答题的个数为 ,试写出
,试写出 的分布列,并求
的分布列,并求 的数学期望。
的数学期望。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题12分)文科班某同学参加广东省学业水平测试,物理、化学、生物获得等级A和获得等级不是A的机会相等,物理、化学、生物获得等级A的事件分别记为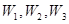 ,物理、化学、生物获得等级不是A的事件分别记为
,物理、化学、生物获得等级不是A的事件分别记为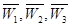 .
.
(I)试列举该同学这次水平测试中物理、化学、生物成绩是否为A的所有可能结果(如三科成绩均为A记为(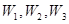 );
);
(II)求该同学参加这次水平测试获得两个A的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
已知集合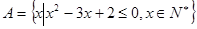 ,集合
,集合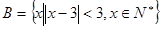 ,
,
集合
(1)列举出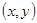 所有可能的结果;
所有可能的结果;
(2)从集合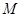 中任取一个元素,求“
中任取一个元素,求“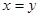 ”的概率
”的概率
(3)从集合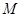 中任取一个元素,求“
中任取一个元素,求“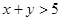 ”的概率.
”的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com