
如图所示,已知D是△ABC中AB边上一点,DE∥BC且交AC于E,EF∥AB且交BC于F,且S△ADE=1,S△EFC=4,则四边形BFED的面积等于多少?

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
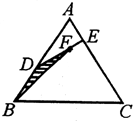 如图所示,已知D是面积为1的△ABC的边AB的中点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设,
如图所示,已知D是面积为1的△ABC的边AB的中点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设,| DF |
| DE |
| AE |
| AC |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
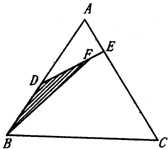 如图所示,已知D是面积为1的△ABC的边AB上的任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设
如图所示,已知D是面积为1的△ABC的边AB上的任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设| AD |
| AB |
| AE |
| AC |
| DF |
| DE |
| 1 |
| 2 |
A、
| ||
B、
| ||
C、
| ||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图所示,已知D是面积为1的△ABC的边AB上任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设
如图所示,已知D是面积为1的△ABC的边AB上任一点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设| AD |
| AB |
| AE |
| AC |
| DF |
| DE |
| 1 |
| 2 |
| a+b+c |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
如图所示,已知D是面积为1的△ABC的边AB的中点,E是边AC上任一点,连接DE,F是线段DE上一点,连接BF,设![]() =λ1,
=λ1,![]() =λ2,且λ1+λ2=
=λ2,且λ1+λ2=![]() ,记△BDF的面积为S=f(λ1,λ2),则S的最大值是________.
,记△BDF的面积为S=f(λ1,λ2),则S的最大值是________.
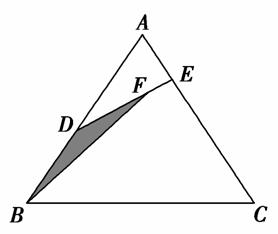
查看答案和解析>>
科目:高中数学 来源:2010年普通高等学校招生全国统一考试(重庆卷)数学理工类模拟试卷(三) 题型:选择题
如图所示,已知D是面积为1的 的边AB上任一点,E是边AC上任一点,连结DE,F是线段DE上一点,连结BF,设
的边AB上任一点,E是边AC上任一点,连结DE,F是线段DE上一点,连结BF,设 ,且
,且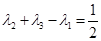 ,记
,记 的面积为
的面积为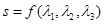 ,则S的最大值是
,则S的最大值是
【注:必要时,可利用定理:若 则
则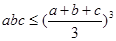 ,
,
(当且仅当 时,取“
时,取“ ”)】
”)】
A. B.
B.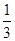 C.
C.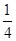 D.
D.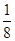
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com