
分析 根据映射和函数的概念,逐一分析3个对应关系,是否满足映射和函数的概念,综合可得答案.
解答 解:(1)A={你班的同学},B={体重},f:每个同学对应自己的体重,任意一个A中元素,在B中均有唯一的元素与之对应,满足映射的概念;但不满足函数的概念;
(2)M={1,2,3,4},N={2,4,6,8},f:n=2m;任意一个M中元素,在N中均有唯一的元素与之对应,满足映射的概念;也满足函数的概念
(3)X=R,Y={非负实数},f:y=x3.任意一个X中元素,例如x=-1,在Y中均没有的元素与之对应,不满足映射的概念;也不满足函数的概念
综上所述:其中是映射的有2个,是函数的有1个,
故答案为:2,1.
点评 本题考查了映射和函数的概念,关键是对映射和函数概念的理解,是基础题.


科目:高中数学 来源: 题型:解答题
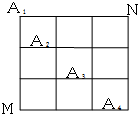 如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.
如图,在某城市中,M,N两地之间有整齐的方格形道路网,A1、A2、A3、A4是道路网中位于一条对角线上的4个交汇处,今甲由道路网M处出发随机地选择一条沿街的最短路径到达N处.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | “?x∈R,使|x|<0” | B. | “?x∈R,使|x|<0” | C. | “?x∉R,使|x|<0” | D. | “?x∈R,使|x|≤0” |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{9}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.
如图,在平面直角坐标系xOy中,以Ox轴为始边作两个锐角α、β,它们的终边分别与单位圆相交于A、B两点.已知A、B的横坐标分别为x1,x2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com