
分析 (1)由题意和三角函数的定义求出sinα和cosα的值;
(2)由题意和正切函数的定义求出tanα,由两角和的正切公式求出答案;
(3)由平方关系将分式化为齐次时,由商的关系化简正切,将(2)中的值代入求值即可.
解答 解(1)由题意知,x=-3,y=4,则r=5,
∴$sinα=\frac{y}{r}=\frac{4}{5},cosα=\frac{x}{r}=-\frac{3}{5}$;…(3分)
(2)∵角α的终边经过点P(-3,4),
∴$tanα=-\frac{4}{3}$,
∴$tan(α+\frac{π}{4})=\frac{1+tanα}{1-tanα}=-\frac{1}{7}$;…(6分)
(3)原式=$\frac{{sin}^{2}(α+\frac{π}{4})+sin(α+\frac{π}{4})•cos(α+\frac{π}{4})}{{sin}^{2}(α+\frac{π}{4})+{cos}^{2}(α+\frac{π}{4})}$
=$\frac{{tan}^{2}(α+\frac{π}{4})+tan(α+\frac{π}{4})}{{tan}^{2}(α+\frac{π}{4})+1}=\frac{\frac{1}{49}-\frac{1}{7}}{\frac{1}{49}+1}=-\frac{3}{25}$…(10分)
点评 本题考查两角和的正切公式,三角函数的定义,及同角三角函数的基本关系的应用,考查化简、变形能力.


 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中数学 来源: 题型:解答题
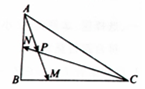 在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$
在△ABC中,$\overrightarrow{AM}$=$\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{4}$$\overrightarrow{AC}$查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 196 | 197 | 200 | 203 | 204 |
| y | 1 | 3 | 6 | 7 | m |
| A. | 8.3 | B. | 8.2 | C. | 8.1 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 外语 | ||||
| 优 | 良 | 及格 | ||
| 数学 | 优 | 8 | m | 9 |
| 良 | 9 | n | 11 | |
| 及格 | 8 | 9 | 11 | |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com