练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

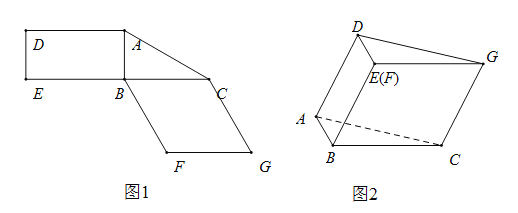
    【题目】图1是由矩形ADEB，Rt△ABC和菱形BFGC组成的一个平面图形，其中AB=1，BE=BF=2，∠FBC=60°，将其沿AB，BC折起使得BE与BF重合，连结DG，如图2.

    （1）证明：图2中的A，C，G，D四点共面，且平面ABC⊥平面BCGE；

    （2）求图2中的二面角BCGA的大小.

    【答案】(1)见详解；(2) .

    【解析】

    (1)因为折纸和粘合不改变矩形，和菱形内部的夹角，所以，依然成立，又因和粘在一起，所以得证.因为是平面垂线，所以易证.(2)在图中找到对应的平面角，再求此平面角即可.于是考虑关于的垂线，发现此垂足与的连线也垂直于.按照此思路即证.

    (1)证：，，又因为和粘在一起.

    ，A，C，G，D四点共面.

    又.

    平面BCGE，平面ABC，平面ABC平面BCGE，得证.

    (2)过B作延长线于H，连结AH，因为AB平面BCGE，所以

    而又，故平面，所以.又因为所以是二面角的平面角，而在中，又因为故，所以.

    而在中,，即二面角的度数为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】一年之计在于春，一日之计在于晨，春天是播种的季节，是希望的开端.某种植户对一块地的个坑进行播种，每个坑播3粒种子，每粒种子发芽的概率均为，且每粒种子是否发芽相互独立.对每一个坑而言，如果至少有两粒种子发芽，则不需要进行补播种，否则要补播种.

    （1）当取何值时，有3个坑要补播种的概率最大？最大概率为多少？

    （2）当时，用表示要补播种的坑的个数，求的分布列与数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，为正三角形，平面平面，，为的中点，．

    （1）求证：；

    （2）求二面角的平面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）解关于的不等式：；

    （2）当时，过点是否存在函数图象的切线？若存在，有多少条？若不存在,说明理由；

    （3）若是使恒成立的最小值，试比较与的大小（）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知动圆过定点，且与直线相切，动圆圆心的轨迹为，过作斜率为的直线与交于两点，过分别作的切线，两切线的交点为，直线与交于两点．

    （1）证明：点始终在直线上且；

    （2）求四边形的面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的短轴长为，离心率，其右焦点为.

    （1）求椭圆的方程；

    （2）过作夹角为的两条直线分别交椭圆于和，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数满足=1，则等于（ ）

    A.-B.C.-D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面向量，满足：||＝2，||＝1．

    （1）若（2）（）＝1，求的值；

    （2）设向量，的夹角为θ．若存在t∈R，使得，求cosθ的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知定义在上的函数，对任意，都有成立，若函数的图象关于直线对称，则

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案