练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，在扇形OAB中，∠AOB=90°，C为
    AB
    的中点．在OC上任取点N，过N作EF⊥OC，交
    AB
    于E．F，则EF＜OA的概率为（　　）
    分析：由于点N随机地落在线段OC上，故可以认为点N落在线段OC上任一点是等可能的，可将线段OC看做区域D，以线段长度为“测度”来计算．
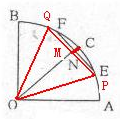    解答：解：如图，当且仅当PQ=OA时，即N点在线段OC上的点M处时，
    △POQ为正三角形，∠MOP=30°，
    设半圆的半径为R，
    则OM=
    		3
    2
    OP    =
    		3
    2
    R
    又因为N对线段OC上的所有的点都是等可能的，
    所以在线段OC上任取一点N，使得ON＞OC?EF＜OA，
    则EF＜OA的概率为：
    MC
    OC
    =
    R-
    		3
    2
    R
    R
    =1-
    		3
    2
    ．
    故答案为：1-
    		3
    2
    ．
    点评：本题主要考查了几何概型，如果每个事件发生的概率只与构成该事件区域的长度（面积或体积）成比例，则称这样的概率模型为几何概率模型，简称为几何概型．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

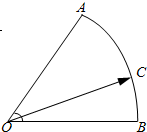    （2013•杭州一模）如图，在扇形OAB中，∠AOB=60°，点C为弧AB上的一个动点．若
    OC
    =x
    OA
    +y
    OB
    ，则x+3y的取值范围是
    [1，3]
    [1，3]
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

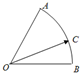
    如图，在扇形OAB中，∠AOB=60°，C为弧AB上且与A，B不重合的一个动点，
    OC
    =x
    OA
    +y
    OB
    ，若u=x+λy，（λ＞0）存在最大值，则λ的取值范围为（　　）

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    如图，在扇形OAB中，∠AOB=60°，C为弧AB上且与A，B不重合的一个动点，
    OC
    =x
    OA
    +y
    OB
    ，若u=x+λy，（λ＞0）存在最大值，则λ的取值范围为（　　）
    A．(
    1
    2
    ，1)    		B．（1，3）C．(
    1
    2
    ，2)    		D．(
    1
    3
    ，3)
    精英家教网

    查看答案和解析>>

    科目：高中数学 来源：2013年浙江省杭州市重点高中高考命题比赛数学参赛试卷01（理科）（解析版） 题型：选择题

    如图，在扇形OAB中，∠AOB=60°，C为弧AB上且与A，B不重合的一个动点，，若u=x+λy，（λ＞0）存在最大值，则λ的取值范围为（ ）

    A．
    B．（1，3）
    C．
    D．

    查看答案和解析>>

    同步练习册答案