
【题目】已知函数y=|x2﹣1|的图象与函数y=kx2﹣(k+2)x+2的图象恰有2个不同的公共点,则实数k的取值范围为 .
【答案】k≤0或k=1或k≥4
【解析】解:函数y=kx2﹣(k+2)x+2=(kx﹣2)(x﹣1)的图象与函数y=|x2﹣1|的图象有1个交点(1,0).
当k<0, ![]() ,函数y=|x2﹣1|的图象与函数y=kx2﹣(k+2)x+2的图象有另外1个不同于(1,0)的交点;
,函数y=|x2﹣1|的图象与函数y=kx2﹣(k+2)x+2的图象有另外1个不同于(1,0)的交点;
由1﹣x2=kx2﹣(k+2)x+2,(x﹣1)[(k+1)x﹣1]=0,x=1时,k=0,方程有唯一的根1,
满足函数y=|x2﹣1|的图象与函数y=kx2﹣(k+2)x+2的图象
恰有2个不同的公共点;
k>0时,由图象可得k=1或k≥4满足题意,
综上所述,k≤0或k=1或k≥4.
所以答案是:k≤0或k=1或k≥4.
【考点精析】通过灵活运用二次函数的性质,掌握当![]() 时,抛物线开口向上,函数在
时,抛物线开口向上,函数在![]() 上递减,在
上递减,在![]() 上递增;当
上递增;当![]() 时,抛物线开口向下,函数在
时,抛物线开口向下,函数在![]() 上递增,在
上递增,在![]() 上递减即可以解答此题.
上递减即可以解答此题.


科目:高中数学 来源: 题型:
【题目】如图,在△ABC中,CD是∠ACB的平分线,△ACD的外接圆交BC于点E,AB=2AC,
(1)求证:BE=2AD;
(2)求函数AC=1,BC=2时,求AD的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直四棱柱A1B1C1D1﹣ABCD中,当底面四边形ABCD满足条件 时,有A1C⊥B1D1 . (注:填上你认为正确的一种条件即可,不必考虑所有可能的情形.)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c.已知acosB﹣c= ![]() .
.
(1)求角A的大小;
(2)若b﹣c= ![]() ,a=3+
,a=3+ ![]() ,求BC边上的高.
,求BC边上的高.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在直三棱柱ABC﹣A1B1C1中,AC=3,BC=4,AB=5,点D是AB的中点. 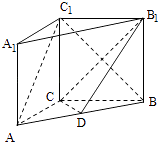
(1)求证:AC⊥BC1;
(2)求证:AC1∥平面CDB1 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体EF﹣ABCD中,ABCD,ABEF均为直角梯形, ![]() ,DCEF为平行四边形,平面DCEF⊥平面ABCD.
,DCEF为平行四边形,平面DCEF⊥平面ABCD. 
(1)求证:DF⊥平面ABCD;
(2)若△ABD是等边三角形,且BF与平面DCEF所成角的正切值为 ![]() ,求二面角A﹣BF﹣C的平面角的余弦值.
,求二面角A﹣BF﹣C的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》是我国古代数学名著,它在几何学中的研究比西方早1千多年.在《九章算术》中,将底面为直角三角形,且侧棱垂直于底面的三棱柱称为堑堵,阳马指底面为矩形,一侧棱垂直于底面的四棱锥,鳖臑指四个面均为直角三角形的四面体.如图,在堑堵ABC﹣A1B1C1中,AC⊥BC. 
(Ⅰ)求证:四棱锥B﹣A1ACC1为阳马;并判断四面体B﹣A1CC1是否为鳖臑,若是,请写出各个面的直角(只要求写出结论).
(Ⅱ)若A1A=AB=2,当阳马B﹣A1ACC1体积最大时,求二面角C﹣A1B﹣C1的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市公租房的房源位于A,B,C,D四个片区,设每位申请人只申请其中一个片区的房源,且申请其中任一个片区的房源是等可能的,在该市的甲、乙、丙三位申请人中:
(1)求恰有1人申请A片区房源的概率;
(2)用x表示选择A片区的人数,求x的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com