
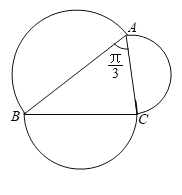
【题目】定义在封闭的平面区域D内任意两点的距离的最大值称为平面区域D的“直径".已知锐角三角形的三个顶点A,B,C在半径为1的圆上,且![]() ,分别以
,分别以![]() 各边为直径向外作三个半圆,这三个半圆和
各边为直径向外作三个半圆,这三个半圆和![]() 构成平面区域D,则平面区域D的“直径”是______.
构成平面区域D,则平面区域D的“直径”是______.
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:高中数学 来源: 题型:
【题目】如图,在三棱柱ABC-A1B1C1中,BB1⊥平面ABC,∠BAC=90°,AC=AB=AA1,E是BC的中点.

(1)求证:AE⊥B1C;
(2)若G为C1C中点,求二面角C-AG-E的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
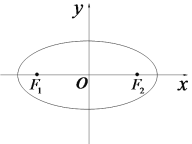
【题目】平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的离心率为
的离心率为![]() ,左、右焦点分别是
,左、右焦点分别是![]() ,以
,以![]() 为圆心以3为半径的圆与以
为圆心以3为半径的圆与以![]() 为圆心以1为半径的圆相交,且交点在椭圆
为圆心以1为半径的圆相交,且交点在椭圆![]() 上.
上.
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 上一动点
上一动点![]() 的直线
的直线![]() ,过F2与x轴垂直的直线记为
,过F2与x轴垂直的直线记为![]() ,右准线记为
,右准线记为![]() ;
;
①设直线![]() 与直线
与直线![]() 相交于点M,直线
相交于点M,直线![]() 与直线
与直线![]() 相交于点N,证明
相交于点N,证明![]() 恒为定值,并求此定值。
恒为定值,并求此定值。
②若连接![]() 并延长与直线
并延长与直线![]() 相交于点Q,椭圆
相交于点Q,椭圆![]() 的右顶点A,设直线PA的斜率为
的右顶点A,设直线PA的斜率为![]() ,直线QA的斜率为
,直线QA的斜率为![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】滨海市政府今年加大了招商引资的力度,吸引外资的数量明显增加.一外商计划在滨海市投资两个项目,总投资20亿元,其中甲项目的10年收益额![]() (单位:亿元)与投资额
(单位:亿元)与投资额![]() (单位:亿元)满足
(单位:亿元)满足![]() ,乙项目的10年收益额
,乙项目的10年收益额![]() (单位:亿元)与投资额
(单位:亿元)与投资额![]() (单位:亿元)满足
(单位:亿元)满足![]() ,并且每个项目至少要投资2亿元.设两个项目的10年收益额之和为
,并且每个项目至少要投资2亿元.设两个项目的10年收益额之和为![]() .
.
(1)求![]() ;
;
(2)如何安排甲、乙两个项目的投资额,才能使这两个项目的10年收益额之和![]() 最大?
最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com