
| A. | (0,1) | B. | ($\frac{1}{4}$,$\frac{1}{2}$) | C. | (0,$\frac{1}{4}$) | D. | ($\frac{1}{2}$,1) |
分析 根据函数f(x)的单调性得出loga(a${\;}^{\frac{x}{2}}$-t)=x有两解,令a${\;}^{\frac{x}{2}}$=m(m>0),则关于m的方程t=m-m2有两解,根据二次函数的性质得出t的范围.
解答 解:∵y=ax-t与y=logax的单调性相同,
∴f(x)=loga(ax-t)(a>0且a≠1)在定义域上是增函数,
∵f(x)区间[$\frac{m}{2}$,$\frac{n}{2}$]上的值域为[m,n],
∴$\left\{\begin{array}{l}{lo{g}_{a}({a}^{\frac{m}{2}}-t)=m}\\{lo{g}_{a}({a}^{\frac{n}{2}}-t)=n}\end{array}\right.$,
∴方程loga(a${\;}^{\frac{x}{2}}$-t)=x有两解,即方程ax=a${\;}^{\frac{x}{2}}$-t有两解,
设a${\;}^{\frac{x}{2}}$=m(m>0),则t=m-m2,
作出t=m-m2(m>0)的函数图象如图所示:
∵方程ax=a${\;}^{\frac{x}{2}}$-t有两解,∴关于m的方程t=m-m2有两解,
∴0<t<$\frac{1}{4}$.
故选C.
点评 本题考查了对数函数,指数函数和二次函数的性质,换元法解题思想,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | $-\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
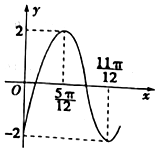 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的图象如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 0 | C. | -1 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
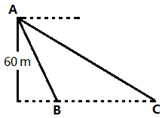 如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )
如图,从气球A上测得正前方的河流的两岸B,C的俯角分别为60o,30°,此时气球的高是60m,则河流的宽度BC等于( )| A. | $30\sqrt{3}$ | B. | $30({\sqrt{3}-1})$ | C. | $40\sqrt{3}$ | D. | $40({\sqrt{3}-1})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若$λ\overrightarrow{a}+μ\overrightarrow{b}$=$\overrightarrow{0}$,则λ=μ=0 | B. | 若$\overrightarrow{a}•\overrightarrow{b}$=0,则$\overrightarrow{a}$∥$\overrightarrow{b}$ | ||
| C. | 若$\overrightarrow{a}$∥$\overrightarrow{b}$,则$\overrightarrow{a}$在$\overrightarrow{b}$上的投影为|$\overrightarrow{a}$| | D. | 若$\overrightarrow{a}⊥\overrightarrow{b}$,则$\overrightarrow{a}$•$\overrightarrow{b}$=($\overrightarrow{a}$$•\overrightarrow{b}$)2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com