
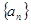 中,已知
中,已知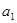 +
+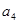 +
+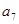 =39,
=39,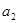 +
+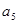 +
+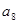 =33,则
=33,则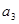 +
+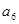 +
+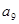 =
=| A.30 | B.27 | C.24 | D.21 |
科目:高中数学 来源:不详 题型:单选题
 (n=1,2,3,…),则下列能使an=a的n的数值是( )
(n=1,2,3,…),则下列能使an=a的n的数值是( )| A.15 | B.16 | C.17 | D.18 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 (n∈N+)
(n∈N+) ,判断数列{bn}的单调性,并证明你的结论
,判断数列{bn}的单调性,并证明你的结论查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
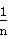 (n≥2),其余每个数是它下一行左右相邻两个数的和,如:
(n≥2),其余每个数是它下一行左右相邻两个数的和,如: 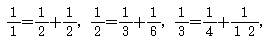
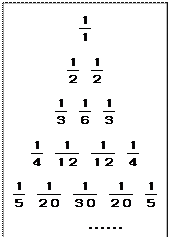
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com