
【题目】已知椭圆C: ![]() 经过点
经过点 ,且离心率为
,且离心率为![]() .
.
(1)求椭圆C的方程;
(2)设直线![]() :
: ![]() 与椭圆C交于两个不同的点A,B,求
与椭圆C交于两个不同的点A,B,求![]() 面积的最大值(O为坐标原点).
面积的最大值(O为坐标原点).
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案科目:高中数学 来源: 题型:
【题目】已知一工厂生产了某种产品700件,该工厂对这些产品进行了安全和环保这两个性能的质量检测。工厂决定利用随机数表法从中抽取100件产品进行抽样检测,现将700件产品按001,002,…,700进行编号;
(1)如果从第8行第4列的数开始向右读,请你依次写出最先检测的3件产品的编号;
(下面摘取了随机数表的第7~9行)
84 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76
63 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 79
33 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 54
(2)抽取的100件产品的安全性能和环保性能的质量检测结果如下表:
检测结果分为优等、合格、不合格三个等级,横向和纵向分别表示安全性能和环保性能。若在该样本中,产品环保性能是优等的概率为![]() ,求
,求![]() ,
,![]() 的值。
的值。
件数 | 环保性能 | |||
优等 | 合格 | 不合格 | ||
安全性能 | 优等 | 6 | 20 | 5 |
合格 | 10 | 18 | 6 | |
不合格 |
| 4 |
| |
(3)已知![]() ,
,![]() ,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
,求在安全性能不合格的产品中,环保性能为优等的件数比不合格的件数少的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() ,其中
,其中![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)已知当![]() (其中
(其中![]() 是自然对数)时,在
是自然对数)时,在![]() 上至少存在一点
上至少存在一点![]() ,使
,使![]() 成立,求
成立,求![]() 的取值范围;
的取值范围;
(3)求证:当![]() 时,对任意
时,对任意![]() ,
, ![]() ,有
,有![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2017年“双节”期间,高速公路车辆较多.某调查公司在一服务区从七座以下小型汽车中按进服务区的先后每间隔50辆就抽取一辆的抽样方法抽取40名驾驶员进行询问调查,将他们在某段高速公路的车速![]() 分成六段:
分成六段: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 后得到如图的频率分布直方图.
后得到如图的频率分布直方图.
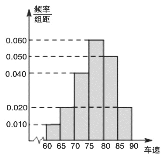
(1)调查公司在采样中,用到的是什么抽样方法?
(2)求这40辆小型车辆车速的众数、中位数及平均数的估计值;
(3)若从车速在![]() 的车辆中任抽取2辆,求车速在
的车辆中任抽取2辆,求车速在![]() 的车辆至少有一辆的概率.
的车辆至少有一辆的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
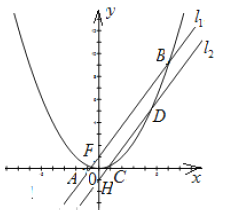
【题目】已知抛物线![]() 上一点
上一点![]() 的纵坐标为4,且点
的纵坐标为4,且点![]() 到焦点
到焦点![]() 的距离为5.
的距离为5.
(1)求抛物线![]() 的方程;
的方程;
(2)设斜率为![]() 的两条平行直线
的两条平行直线![]() 分别经过点
分别经过点![]() 和
和![]() ,如图.
,如图. ![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,
两点, ![]() 与抛 物线
与抛 物线![]() 交
交![]() 两点.问:是否存在实数
两点.问:是否存在实数![]() ,使得四边形
,使得四边形![]() 的面积为
的面积为![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是不重合直线,
是不重合直线,![]() 是不重合平面,则下列命题
是不重合平面,则下列命题
①若![]() ,则
,则![]() ∥
∥![]()
②若![]() ∥
∥![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
③若![]() ∥
∥![]() 、
、![]() ∥
∥![]() ,则
,则![]() ∥
∥![]()
④若![]() ,则
,则![]() ∥
∥![]()
⑤若![]() ,则
,则![]() ∥
∥![]()
为假命题的是
A. ①②③ B. ①②⑤ C. ③④⑤ D. ①②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知在平面直角坐标系中,直线l过点P(1,2).
(1)若直线l在x轴和y轴上的截距相等,求直线l的方程;
(2)求坐标原点O到直线l距离取最大值时的直线l的方程;
(3)设直线l与x轴正半轴、y轴正半轴分别相交于A,B两点,当|PA||PB|最小时,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com