
分析 设出对称点的坐标,利用点的对称的关系建立方程关系进行求解即可.
解答 解:设对称点的坐标为(x,y),
则满足$\left\{\begin{array}{l}{\frac{y-1}{x+2}•(-1)=-1}\\{\frac{x-2}{2}+\frac{1+y}{2}-3=0}\end{array}\right.$,
即$\left\{\begin{array}{l}{y-1=x+2}\\{x+y-7=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=2}\\{y=5}\end{array}\right.$,即对称点的坐标为(2,5),
故答案为:(2,5).
点评 本题主要考查点的对称的应用,根据对称关系建立方程是解决本题的关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
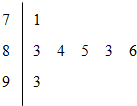 某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )
某学校2012年五四青年节举办十佳歌手赛,如图是七位评委为某选手打出的分数的茎叶图,去掉一个最高分和一个最低分后,所剩数据的众数数与中位数分别为( )| A. | 83,83 | B. | 83,83.5 | C. | 83,84 | D. | 84,83 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x0∈R,sinx0≥1 | B. | ¬p:?x∈R,sinx≥1 | ||
| C. | ¬p:?x0∈R,sinx0>1 | D. | ¬p:?x∈R,sinx>1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},2})$ | B. | (-1,2) | C. | $[{\frac{1}{2},2}]$ | D. | [-1,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,2,3,4} | B. | {2,3,4} | C. | {3,4} | D. | {x|2<x≤4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com