
【题目】滨海市政府今年加大了招商引资的力度,吸引外资的数量明显增加.一外商计划在滨海市投资两个项目,总投资20亿元,其中甲项目的10年收益额![]() (单位:亿元)与投资额
(单位:亿元)与投资额![]() (单位:亿元)满足
(单位:亿元)满足![]() ,乙项目的10年收益额
,乙项目的10年收益额![]() (单位:亿元)与投资额
(单位:亿元)与投资额![]() (单位:亿元)满足
(单位:亿元)满足![]() ,并且每个项目至少要投资2亿元.设两个项目的10年收益额之和为
,并且每个项目至少要投资2亿元.设两个项目的10年收益额之和为![]() .
.
(1)求![]() ;
;
(2)如何安排甲、乙两个项目的投资额,才能使这两个项目的10年收益额之和![]() 最大?
最大?
科目:高中数学 来源: 题型:
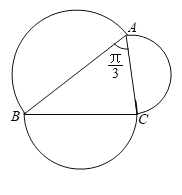
【题目】定义在封闭的平面区域D内任意两点的距离的最大值称为平面区域D的“直径".已知锐角三角形的三个顶点A,B,C在半径为1的圆上,且![]() ,分别以
,分别以![]() 各边为直径向外作三个半圆,这三个半圆和
各边为直径向外作三个半圆,这三个半圆和![]() 构成平面区域D,则平面区域D的“直径”是______.
构成平面区域D,则平面区域D的“直径”是______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】司机在开机动车时使用手机是违法行为,会存在严重的安全隐患,危及自己和他人的生命.为了研究司机开车时使用手机的情况,交警部门调查了100名机动车司机,得到以下统计:在55名男性司机中,开车时使用手机的有40人,开车时不使用手机的有15人;在45名女性司机中,开车时使用手机的有20人,开车时不使用手机的有25人.
(1)完成下面的2×2列联表,并判断是否有99.5%的把握认为开车时使用手机与司机的性别有关;

(2)以上述的样本数据来估计总体,现交警部门从道路上行驶的大量机动车中随机抽检3辆,记这3辆车中司机为男性且开车时使用手机的车辆数为X,若每次抽检的结果都相互独立,求X的分布列和数学期望E(X).
参考公式与数据:![]() ,其中n=a+b+c+d.
,其中n=a+b+c+d.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 过点
过点![]() ,且圆心在直线
,且圆心在直线![]() 上.
上.
(1)求圆![]() 的方程;
的方程;
(2)平面上有两点![]() ,点
,点![]() 是圆
是圆![]() 上的动点,求
上的动点,求![]() 的最小值;
的最小值;
(3)若![]() 是
是![]() 轴上的动点,
轴上的动点,![]() 分别切圆
分别切圆![]() 于
于![]() 两点,试问:直线
两点,试问:直线![]() 是否恒过定点?若是,求出定点坐标,若不是,说明理由.
是否恒过定点?若是,求出定点坐标,若不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】平面上给定![]() 及点
及点![]() ,构造点列
,构造点列![]() ,
,![]() ,
,![]() ,…,使得
,…,使得![]() 为点
为点![]() 绕中心
绕中心![]() 顺时针旋转
顺时针旋转![]() 时所到达的位置,而
时所到达的位置,而![]() 和
和![]() 为点
为点![]() 和
和![]() 分别绕中心
分别绕中心![]() 和
和![]() 顺时针旋转
顺时针旋转![]() 时所到达的位置,
时所到达的位置,![]() .若对某个
.若对某个![]() ,有
,有![]() ,试求
,试求![]() 的各个内角的度数及三个顶点
的各个内角的度数及三个顶点![]() ,
,![]() ,
,![]() 的排列方向.
的排列方向.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,![]() 是由两个全等的菱形
是由两个全等的菱形![]() 和
和![]() 组成的空间图形,
组成的空间图形,![]() ,∠BAF=∠ECD=60°.
,∠BAF=∠ECD=60°.
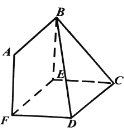
(1)求证:![]() ;
;
(2)如果二面角B-EF-D的平面角为60°,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,前n项和为
,前n项和为![]() ,对任意的正整数n,都有
,对任意的正整数n,都有![]() 恒成立.
恒成立.
(1)求数列![]() 的通项公式;
的通项公式;
(2)已知关于n的不等式![]() …
…![]() 对一切
对一切![]() 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(3)已知 ,数列
,数列![]() 的前n项和为
的前n项和为![]() ,试比较
,试比较![]() 与
与![]() 的大小并证明.
的大小并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com