
【题目】已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的图象在
的图象在![]() 处的切线方程;
处的切线方程;
(2)当![]() 时,求证:
时,求证:![]() 在
在![]() 上有唯一零点.
上有唯一零点.
科目:高中数学 来源: 题型:
【题目】某超市在节日期间进行有奖促销,规定凡在该超市购物满400元的顾客,均可获得一次摸奖机会.摸奖规则如下:奖盒中放有除颜色不同外其余完全相同的4个球(红、黄、黑、白).顾客不放回的每次摸出1个球,若摸到黑球则摸奖停止,否则就继续摸球.按规定摸到红球奖励20元,摸到白球或黄球奖励10元,摸到黑球不奖励.
(1)求1名顾客摸球2次摸奖停止的概率;
(2)记X为1名顾客摸奖获得的奖金数额,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
,椭圆C上任意一点到椭圆两个焦点的距离之和为6.
(1)求椭圆C的方程;
(2)设直线上![]() 与椭圆C交于A,B两点,点
与椭圆C交于A,B两点,点![]() ,且
,且![]() ,求直线l的方程.
,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:
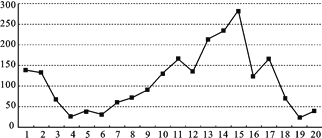
下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com