
【题目】已知双曲线 C 经过点 (2,3),它的渐近线方程为 y = ±![]() .椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
.椭圆 C1与双曲线 C有相同的焦点,椭圆 C1的短轴长与双曲线 C 的实轴长相等.
(1)求双曲线 C 和椭圆 C1 的方程;
(2)经过椭圆 C1 左焦点 F 的直线 l 与椭圆 C1 交于 A、B 两点,是否存在定点 D ,使得无论 AB 怎样运动,都有∠ADF = ∠BDF ?若存在,求出 D 点坐标;若不存在,请说明理由.
【答案】(1)![]() ;
;![]() (2)存在点D
(2)存在点D ![]()
【解析】
(1)双曲线![]() 的方程为:
的方程为:![]() ,则
,则![]() .设椭圆
.设椭圆![]() 的方程;
的方程;![]() 椭圆
椭圆![]() 的短轴长与双曲线
的短轴长与双曲线![]() 的实轴长相等,椭圆
的实轴长相等,椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() 即可得
即可得![]() 、
、![]() 、
、![]()
(2)直线![]() 垂直
垂直![]() 轴时,
轴时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,要使
轴对称,要使![]() ,则点
,则点![]() 必在
必在![]() 轴上,设
轴上,设![]() ,直线
,直线![]() 不垂直
不垂直![]() 轴时,
轴时,![]() 的方程设为:
的方程设为:![]() ,设
,设![]() ,
,![]() ,
,![]() ,
,![]() ,联立
,联立![]() 得
得![]() .要使
.要使![]() ,即直线
,即直线![]() 、
、![]() 的斜率互为相反数,即
的斜率互为相反数,即![]() ,求得
,求得![]()
解:(1)双曲线![]() 方程为:
方程为:![]() ,则
,则![]() .
.
![]() 双曲线
双曲线![]() 的方程为
的方程为![]() .
.
设椭圆![]() 的方程;
的方程;![]()
椭圆![]() 的短轴长与双曲线
的短轴长与双曲线![]() 的实轴长相等,
的实轴长相等,
![]() 椭圆
椭圆![]() 的短轴长为
的短轴长为![]() ,椭圆
,椭圆![]() 与双曲线
与双曲线![]() 有相同的焦点
有相同的焦点![]() ,
,
即![]() ,
,![]() ,椭圆
,椭圆![]() 的方程为:
的方程为:![]() ;
;
(2)直线![]() 垂直
垂直![]() 轴时,
轴时,![]() 、
、![]() 两点关于
两点关于![]() 轴对称,
轴对称,
![]() ,
,![]() 要使
要使![]() ,则点
,则点![]() 必在
必在![]() 轴上,
轴上,
设![]() ,直线
,直线![]() 不垂直
不垂直![]() 轴时,
轴时,![]() 的方程设为:
的方程设为:![]() ,
,
设![]() ,
,![]() ,
,![]() ,
,![]() ,联立
,联立![]() 得
得![]() .
.
![]()
![]() .
.
![]() ,
,![]() 直线
直线![]() 、
、![]() 的斜率互为相反数,
的斜率互为相反数,
即![]() ,
,
![]() 时恒成立.
时恒成立.
![]() 时,
时,![]() ;
;
![]() 存在定点
存在定点![]() ,
,![]() ,使得无论
,使得无论![]() 怎样运动,都有
怎样运动,都有![]() .
.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:
【题目】A地的天气预报显示,A地在今后的三天中,每一天有强浓雾的概率为![]() ,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生
,现用随机模拟的方法估计这三天中至少有两天有强浓雾的概率,先利用计算器产生![]() 之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
之间整数值的随机数,并用0,1,2,3,4,5,6表示没有强浓雾,用7,8,9表示有强浓雾,再以每3个随机数作为一组,代表三天的天气情况,产生了如下20组随机数:
402 978 191 925 273 842 812 479 569 683
231 357 394 027 506 588 730 113 537 779
则这三天中至少有两天有强浓雾的概率近似为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某市10月1日至14日的空气质量指数趋势图,空气质量指数越小表示空气质量越好,空气质量指数小于100表示空气质量优良,下列叙述中不正确的是( )
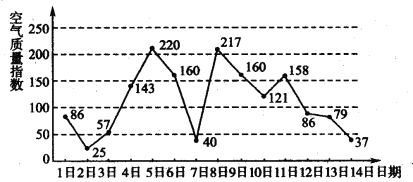
A.这14天中有7天空气质量优良
B.这14天中空气质量指数的中位数是103
C.从10月11日到10月14日,空气质量越来越好
D.连续三天中空气质量指数方差最大的是10月5日至10月7日
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知无穷数列![]() 的各项都是正数,其前
的各项都是正数,其前![]() 项和为
项和为![]() ,且满足:
,且满足:![]() ,
,![]() ,其中
,其中![]() ,常数
,常数![]()
![]() .
.
(1)求证:![]() 是一个定值;
是一个定值;
(2)若数列![]() 是一个周期数列(存在正整数
是一个周期数列(存在正整数![]() ,使得对任意
,使得对任意![]() ,都有
,都有![]() 成立,则称
成立,则称![]() 为周期数列,
为周期数列,![]() 为它的一个周期),求该数列的最小周期;
为它的一个周期),求该数列的最小周期;
(3)若数列![]() 是各项均为有理数的等差数列,
是各项均为有理数的等差数列,![]() (
(![]() ),问:数列
),问:数列![]() 中的所有项是否都是数列
中的所有项是否都是数列![]() 中的项?若是,请说明理由;若不是,请举出反例.
中的项?若是,请说明理由;若不是,请举出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 的极坐标方程;
的极坐标方程;
(2)将曲线![]() 上所有点的横坐标不变,纵坐标缩短到原来的
上所有点的横坐标不变,纵坐标缩短到原来的![]() 倍,得到曲线
倍,得到曲线![]() ,若
,若![]() 与
与![]() 的交点为
的交点为![]() (异于坐标原点
(异于坐标原点![]() ),
),![]() 与
与![]() 的交点为
的交点为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 与椭圆
与椭圆![]() 相交于点M(0,1),N(0,-1),且椭圆的离心率为
相交于点M(0,1),N(0,-1),且椭圆的离心率为![]() .
.
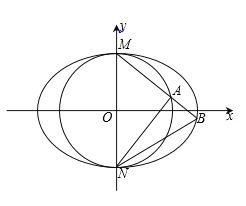
(1)求![]() 的值和椭圆C的方程;
的值和椭圆C的方程;
(2)过点M的直线![]() 交圆O和椭圆C分别于A,B两点.
交圆O和椭圆C分别于A,B两点.
①若![]() ,求直线
,求直线![]() 的方程;
的方程;
②设直线NA的斜率为![]() ,直线NB的斜率为
,直线NB的斜率为![]() ,问:
,问:![]() 是否为定值? 如果是,求出定值;如果不是,说明理由.
是否为定值? 如果是,求出定值;如果不是,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,动点P与定点![]() 的距离和它到定直线
的距离和它到定直线![]() 的距离之比是
的距离之比是![]() ,设动点P的轨迹为E.
,设动点P的轨迹为E.
(1)求动点P的轨迹E的方程;
(2)设过F的直线交轨迹E的弦为AB,过原点的直线交轨迹E的弦为CD,若![]() ,求证:
,求证:![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,D是AC的中点,四边形BDEF是菱形,平面![]() 平面ABC,
平面ABC,![]() ,
,![]() ,
,![]() .
.

![]() 若点M是线段BF的中点,证明:
若点M是线段BF的中点,证明:![]() 平面AMC;
平面AMC;
![]() 求平面AEF与平面BCF所成的锐二面角的余弦值.
求平面AEF与平面BCF所成的锐二面角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com