
| A. |  | B. |  | ||
| C. |  | D. |  |
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
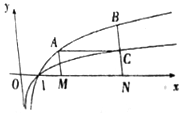 如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.
如图,过函数f(x)=logcx(c>1)的图象上的两点A,B作x轴的垂线,垂足分别为M(a,0),N(b,0)(b>a>1),线段BN与函数g(x)=logmx(m>c>1)的图象交于点C,且AC与x轴平行.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 劳动生产率为1 000元时,工人工资为130元 | |
| B. | 劳动生产率提高1 000元时,工人工资平均提高80元 | |
| C. | 劳动生产率提高1 000元时,工人工资平均提高130元 | |
| D. | 当月工资为250元时,劳动生产率为2 000元 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 2 | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{4}$,1) | B. | (2,+∞) | C. | $({-∞,-2})∪({\frac{1}{4},+∞})$ | D. | $({-∞,\frac{1}{4}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com