练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在平面直角坐标系xoy中，以坐标原点O为极点，x轴正半轴为极轴建立极坐标系。已知曲线C的极坐标方程为，过点的直线l的参数方程为（为参数），直线l与曲线C交于M、N两点。

    （1）写出直线l的普通方程和曲线C的直角坐标方程：

    （2）若成等比数列，求a的值。

    【答案】（1）l的普通方程；C的直角坐标方程；（2）.

    【解析】

    （1）利用极坐标与直角坐标的互化公式即可把曲线的极坐标方程化为直角坐标方程，利用消去参数即可得到直线的直角坐标方程；

    （2）将直线的参数方程，代入曲线的方程，利用参数的几何意义即可得出，从而建立关于的方程，求解即可．

    （1）由直线l的参数方程消去参数t得,

    ，即为l的普通方程

    由，两边乘以得

    为C的直角坐标方程.

    （2）将代入抛物线得

    由已知成等比数列，

    即，，，

    整理得

    （舍去）或.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】下列四个结论：

    ①命题“”的否定是“”；

    ②若是真命题，则可能是真命题；

    ③“且”是“”的充要条件；

    ④当时，幂函数在区间上单调递减.

    其中正确的是

    A. ①③ B. ②④ C. ①④ D. ②③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知空间几何体ABCDE中，△BCD与△CDE均是边长为2的等边三角形，△ABC是腰长为3的等腰三角形，平面CDE⊥平面BCD，平面ABC⊥平面BCD.

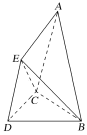
    (1)试在平面BCD内作一条直线，使得直线上任意一点F与E的连线EF均与平面ABC平行，并给出证明；

    (2)求三棱锥E－ABC的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在△ABC中，角A，B，C的对边分别为a，b，c，已知4(tanA＋tanB)＝＋，则cosC的最小值为__________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

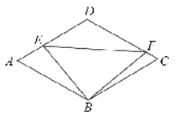
    【题目】如图，郊外有一边长为200m的菱形池塘ABCD，塘边AB与AD的夹角为60°，拟架设三条网隔BE，BF，EF，把池塘分成几个不同区域，其中网隔BE与BF相互垂直，E，F两点分别在塘边AD和DC上，区域BEF为荷花种植区域．记∠ABE＝，荷花种植区域的面积为Sm2．

    （1）求S关于的函数关系式；

    （2）求S的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图（1）在等腰直角三角形中，，将沿中位线翻折得到如图（2）所示的空间图形，使二面角的大小为.

    （1）求证：平面平面；

    （2）若，求直线与平面所成角的正弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】P为双曲线右支上一点，M、N分别是圆上的点，则|PM|-|PN|的最大值为

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】一只青蛙从数轴的原点出发，当投下的硬币正面向上时，它沿数轴的正方向跳动两个单位；当投下的硬币反面向上时，它沿数轴的负方向跳动一个单位，若青蛙跳动次停止，设停止时青蛙在数轴上对应的坐标为随机变量，则______．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂生产某种产品的年固定成本为200万元，每生产千件，需另投入成本为，当年产量不足80千件时，（万元）．当年产量不小于80千件时，（万元）．每件商品售价为0.05万元．通过市场分析，该厂生产的商品能全部售完．

    （1）写出年利润（万元）关于年产量（千件）的函数解析式；

    （2）当年产量为多少千件时，该厂在这一商品的生产中所获利润最大？

    查看答案和解析>>

    同步练习册答案