
【题目】若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足:
分别满足: ![]() 和
和![]() ,则称直线
,则称直线![]() 为
为![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
, ![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的极值;
的极值;
(2)函数![]() 和
和![]() 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
【答案】(1)当![]() 时,
时, ![]() 取极小值,其极小值为
取极小值,其极小值为![]() (2)函数
(2)函数![]() 和
和![]() 存在唯一的隔离直线
存在唯一的隔离直线![]()
【解析】试题分析:(1)由已知中函数f(x)和φ(x)的解析式,求出函数F(x)的解析式,根据求导公式,求出函数的导数,根据导数判断函数的单调性并求极值;(2)由(1)可知,函数f(x)和φ(x)的图象在(![]() ,e)处相交,即f(x)和φ(x)若存在隔离直线,那么该直线必过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-
,e)处相交,即f(x)和φ(x)若存在隔离直线,那么该直线必过这个公共点,设隔离直线的斜率为k.则隔离直线方程为y-e=k(x-![]() ),即y=kx-k
),即y=kx-k![]() +e,根据隔离直线的定义,构造方程,可求出k值,进而得到隔离直线方程
+e,根据隔离直线的定义,构造方程,可求出k值,进而得到隔离直线方程
试题解析:(1)![]()
![]() ,
,
 .
.
当![]() 时,
时, ![]() .
.![]() 当
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递减;
递减;
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递增;
递增;
∴当![]() 时,
时, ![]() 取极小值,其极小值为
取极小值,其极小值为![]() .
.
(2)解法一:由(1)可知函数![]() 和
和![]() 的图象在
的图象在![]() 处有公共点,因此若存在
处有公共点,因此若存在![]() 和
和![]() 的隔离直线,则该直线过这个公共点.
的隔离直线,则该直线过这个公共点.
设隔离直线的斜率为![]() ,则直线方程为
,则直线方程为![]() ,即
,即![]() .
.
由![]() ,可得
,可得![]() 当
当![]() 时恒成立.
时恒成立.
![]() ,
,
![]() 由
由![]() ,得
,得![]() .
.
下面证明![]() 当
当![]() 时恒成立.
时恒成立.
令![]()
![]() ,则
,则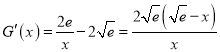 ,
,
当![]() 时,
时, ![]() .
.
![]() 当
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递增;
递增;
当![]() 时,
时, ![]() ,此时函数
,此时函数![]() 递减;
递减;
∴当![]() 时,
时, ![]() 取极大值,其极大值为
取极大值,其极大值为![]() .
.
从而![]() ,即
,即![]() 恒成立.
恒成立.
∴函数![]() 和
和![]() 存在唯一的隔离直线
存在唯一的隔离直线![]() .
.
解法二:由(Ⅰ)可知当![]() 时,
时, ![]() (当且当
(当且当![]() 时取等号).
时取等号).
若存在![]() 和
和![]() 的隔离直线,则存在实常数
的隔离直线,则存在实常数![]() 和
和![]() ,使得
,使得![]() 和
和![]() 恒成立,令
恒成立,令![]() ,则
,则![]() 且
且![]()
![]() ,即
,即![]() .后面解题步骤同解法一.
.后面解题步骤同解法一.


科目:高中数学 来源: 题型:
【题目】已知对任意平面向量 ![]() =(x,y),把
=(x,y),把 ![]() 绕其起点沿逆时针方向旋转θ角得到的向量
绕其起点沿逆时针方向旋转θ角得到的向量 ![]() =(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
=(xcosθ﹣ysinθ,xsinθ+ycosθ),叫做把点B绕点A逆时针方向旋转θ得到点P.
(1)已知平面内点A(2,3),点B(2+2 ![]() ,1).把点B绕点A逆时针方向旋转
,1).把点B绕点A逆时针方向旋转 ![]() 角得到点P,求点P的坐标.
角得到点P,求点P的坐标.
(2)设平面内曲线C上的每一点绕坐标原点沿顺时针方向旋转 ![]() 后得到的点的轨迹方程是曲线y=
后得到的点的轨迹方程是曲线y= ![]() ,求原来曲线C的方程.
,求原来曲线C的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0, ![]() )的部分图象如图所示.
)的部分图象如图所示. 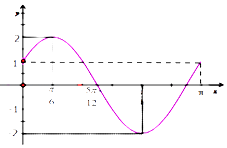
(1)求函数f(x)的解析式;
(2)求函数f(x)的单调递增区间和对称中心.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求函数![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)把![]() 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再把得到的图象向左平移![]() 个单位,得到函数
个单位,得到函数![]() 的图象,求
的图象,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com