
【题目】设数列![]() (
(![]() )的各项均为正整数,且
)的各项均为正整数,且![]() .若对任意
.若对任意![]() ,存在正整数
,存在正整数![]() 使得
使得![]() ,则称数列
,则称数列![]() 具有性质
具有性质![]() .
.
(1)判断数列![]() 与数列
与数列![]() 是否具有性质
是否具有性质![]() ;(只需写出结论)
;(只需写出结论)
(2)若数列![]() 具有性质
具有性质![]() ,且
,且![]() ,
,![]() ,
,![]() ,求
,求![]() 的最小值;
的最小值;
(3)若集合![]() ,且
,且![]() (任意
(任意![]() ,
,![]() ).求证:存在
).求证:存在![]() ,使得从
,使得从![]() 中可以选取若干元素(可重复选取)组成一个具有性质
中可以选取若干元素(可重复选取)组成一个具有性质![]() 的数列.
的数列.
【答案】(1)数列![]() 不具有性质
不具有性质![]() ;数列
;数列![]() 具有性质
具有性质![]() (2)
(2)![]() 的最小值为
的最小值为![]() (3)证明见解析
(3)证明见解析
【解析】
(1)![]() 不满足存在正整数
不满足存在正整数![]() 使得
使得![]() ,故数列
,故数列![]() 不具有性质
不具有性质![]() ;根据定义可知数列
;根据定义可知数列![]() 具有性质
具有性质![]() ;
;
(2)由题可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,所以
,所以![]() ,再验证可知
,再验证可知![]() 时,数列
时,数列![]() 不具有性质
不具有性质![]() ,
,![]() 时,数列
时,数列![]() 具有性质
具有性质![]() ,从而可知
,从而可知![]() 的最小值为
的最小值为![]() ;
;
(3)反证法:假设结论不成立,即对任意![]() 都有:若正整数
都有:若正整数![]() ,则
,则![]() ,再根据定义推出矛盾,从而可证结论正确.
,再根据定义推出矛盾,从而可证结论正确.
(1)数列![]() 不具有性质
不具有性质![]() ;数列
;数列![]() 具有性质
具有性质![]() .
.
(2)由题可知![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
若![]() ,因为
,因为![]() 且
且![]() ,所以
,所以![]() .
.
同理,![]()
因为数列各项均为正整数,所以![]() .所以数列前三项为
.所以数列前三项为![]() .
.
因为数列![]() 具有性质
具有性质![]() ,
,![]() 只可能为
只可能为![]() 之一,而又因为
之一,而又因为![]() ,
,
所以![]() .
.
同理,有![]() .
.
此时数列为![]() .
.
但数列中不存在![]() 使得
使得![]() ,所以该数列不具有性质
,所以该数列不具有性质![]() .
.
所以![]() .
.
当![]() 时,取
时,取![]() .(构造数列不唯一)
.(构造数列不唯一)
经验证,此数列具有性质![]() .
.
所以,![]() 的最小值为
的最小值为![]() .
.
(3)反证法:假设结论不成立,即对任意![]() 都有:若正整数
都有:若正整数![]() ,则
,则![]() .
.
否则,存在![]() 满足:存在
满足:存在![]() ,
,![]() 使得
使得![]() ,此时,从
,此时,从![]() 中取出
中取出![]() :
:
当![]() 时,
时,![]() 是一个具有性质
是一个具有性质![]() 的数列;
的数列;
当![]() 时,
时,![]() 是一个具有性质
是一个具有性质![]() 的数列;
的数列;
当![]() 时,
时,![]() 是一个具有性质
是一个具有性质![]() 的数列.
的数列.
(i)由题意可知,这![]() 个集合中至少有一个集合的元素个数不少于
个集合中至少有一个集合的元素个数不少于![]() 个,
个,
不妨设此集合为![]() ,从
,从![]() 中取出
中取出![]() 个数,记为
个数,记为![]() ,且
,且![]() .
.
令集合![]() .
.
由假设,对任意![]() ,
,![]() ,所以
,所以![]() .
.
(ii)在![]() 中至少有一个集合包含
中至少有一个集合包含![]() 中的至少
中的至少![]() 个元素,不妨设这个集合为
个元素,不妨设这个集合为![]() ,
,
从![]() 中取出
中取出![]() 个数,记为
个数,记为![]() ,且
,且![]() .
.
令集合![]() .
.
由假设![]() .对任意
.对任意![]() ,存在
,存在![]() 使得
使得![]() .
.
所以对任意![]() ,
,![]() ,
,
由假设![]() ,所以
,所以![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(iii)在![]() 中至少有一个集合包含
中至少有一个集合包含![]() 中的至少
中的至少![]() 个元素,不妨设这个集合为
个元素,不妨设这个集合为![]() ,
,
从![]() 中取出
中取出![]() 个数,记为
个数,记为![]() ,且
,且![]() .
.
令集合![]() .
.
由假设![]() .对任意
.对任意![]() ,存在
,存在![]() 使得
使得![]() .
.
所以对任意![]() ,
,![]() ,
,
同样,由假设可得![]() ,所以
,所以![]() ,所以
,所以![]() .
.
(iv)类似地,在![]() 中至少有一个集合包含
中至少有一个集合包含![]() 中的至少
中的至少![]() 个元素,不妨设这个集合为
个元素,不妨设这个集合为![]() ,
,
从![]() 中取出
中取出![]() 个数,记为
个数,记为![]() ,且
,且![]() ,
,
则![]() .
.
(v)同样,在![]() 中至少有一个集合包含
中至少有一个集合包含![]() 中的至少
中的至少![]() 个元素,不妨设这个集合为
个元素,不妨设这个集合为![]() ,
,
从![]() 中取出
中取出![]() 个数,记为
个数,记为![]() ,且
,且![]() ,同理可得
,同理可得![]() .
.
(vi)由假设可得![]() .
.
同上可知,![]() ,
,
而又因为![]() ,所以
,所以![]() ,矛盾.所以假设不成立.
,矛盾.所以假设不成立.
所以原命题得证.


 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线l的参数方程为![]() (t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为
(t为参数),若以O为极点,x轴的正半轴为极轴且取相同的单位长度建立极坐标系,曲线C的极坐标方程为![]() .
.
(1)求曲线C的直角坐标方程及直线l的普通方程;
(2)将所得曲线C向右平移1个单位长度,再将曲线C上的所有点的横坐标变为原来的2倍,得到曲线![]() ,求曲线
,求曲线![]() 上的点到直线l的距离的最大值.
上的点到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的普通方程为:
的普通方程为:![]() ,以坐标原点为极点,
,以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,正方形
,正方形![]() 的顶点都在
的顶点都在![]() 上,且
上,且![]() 逆时针依次排列,点
逆时针依次排列,点![]() 的极坐标为
的极坐标为![]()
(1)写出曲线![]() 的参数方程,及点
的参数方程,及点![]() 的直角坐标;
的直角坐标;
(2)设![]() 为椭圆
为椭圆![]() 上的任意一点,求:
上的任意一点,求:![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设点![]() 是抛物线
是抛物线![]() 的焦点,直线
的焦点,直线![]() 与抛物线
与抛物线![]() 相切于点
相切于点![]() (点
(点![]() 位于第一象限),并与抛物线
位于第一象限),并与抛物线![]() 的准线相交于点
的准线相交于点![]() .过点
.过点![]() 且与直线
且与直线![]() 垂直的直线
垂直的直线![]() 交抛物线
交抛物线![]() 于另一点
于另一点![]() ,交
,交![]() 轴于点
轴于点![]() ,连结
,连结![]() .
.
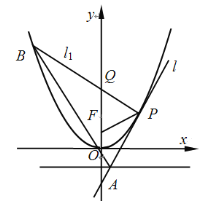
(1)证明:![]() 为等腰三角形;
为等腰三角形;
(2)求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多寓意美好的曲线,曲线![]() 被称为“四叶玫瑰线”(如图所示).
被称为“四叶玫瑰线”(如图所示).

给出下列三个结论:
①曲线![]() 关于直线
关于直线![]() 对称;
对称;
②曲线![]() 上任意一点到原点的距离都不超过
上任意一点到原点的距离都不超过![]() ;
;
③存在一个以原点为中心、边长为![]() 的正方形,使得曲线
的正方形,使得曲线![]() 在此正方形区域内(含边界).
在此正方形区域内(含边界).
其中,正确结论的序号是________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列结论中正确的个数是( )
①在![]() 中,“
中,“![]() ”是“
”是“![]() ”的必要不充分条件;
”的必要不充分条件;
②若![]() ,
,![]() 的最小值为2;
的最小值为2;
③夹在圆柱的两个平行截面间的几何体是圆柱;
④数列![]() 的通项公式为
的通项公式为![]() ,则数列的前
,则数列的前![]() 项和
项和![]() .( )
.( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了实施“科技下乡,精准脱贫”战略,某县科技特派员带着![]() 三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择
三个农业扶贫项目进驻某村,对仅有的四个贫困户进行产业帮扶.经过前期走访得知,这四个贫困户甲、乙、丙、丁选择![]() 三个项目的意向如下:
三个项目的意向如下:
扶贫项目 |
|
|
|
贫困户 | 甲、乙、丙、丁 | 甲、乙、丙 | 丙、丁 |
若每个贫困户只能从自己已登记的选择意向中随机选取一项,且每个项目至多有两个贫困户选择,则甲乙两户选择同一个扶贫项目的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近期,西安公交公司分别推出支付宝和微信扫码支付乘车活动,活动设置了一段时间的推广期,由于推广期内优惠力度较大,吸引越来越多的人开始使用扫码支付.某线路公交车队统计了活动刚推出一周内每一天使用扫码支付的人次,![]() 表示活动推出的天数,
表示活动推出的天数,![]() 表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
表示每天使用扫码支付的人次(单位:十人次),统计数据如表下所示:
![]()
根据以上数据,绘制了散点图.
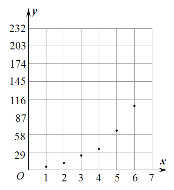
(1)根据散点图判断,在推广期内,![]() 与
与![]() (
(![]() 均为大于零的常数),哪一个适宜作为扫码支付的人次
均为大于零的常数),哪一个适宜作为扫码支付的人次![]() 关于活动推出天数
关于活动推出天数![]() 的回归方程类型?(给出判断即可,不必说明理由);
的回归方程类型?(给出判断即可,不必说明理由);
(2)根据(1)的判断结果及表1中的数据,建立![]() 与
与![]() 的回归方程,并预测活动推出第8天使用扫码支付的人次;
的回归方程,并预测活动推出第8天使用扫码支付的人次;
(3)推广期结束后,车队对乘客的支付方式进行统计,结果如下表:
![]()
西安公交六公司车队为缓解周边居民出行压力,以![]() 万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为
万元的单价购进了一批新车,根据以往的经验可知,每辆车每个月的运营成本约为![]() 万元.已知该线路公交车票价为
万元.已知该线路公交车票价为![]() 元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受
元,使用现金支付的乘客无优惠,使用乘车卡支付的乘客享受![]() 折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有
折优惠,扫码支付的乘客随机优惠,根据统计结果得知,使用扫码支付的乘客中有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受
的概率享受![]() 折优惠,有
折优惠,有![]() 的概率享受
的概率享受![]() 折优惠.预计该车队每辆车每个月有
折优惠.预计该车队每辆车每个月有![]() 万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要
万人次乘车,根据所给数据以事件发生的频率作为相应事件发生的概率,在不考虑其它因素的条件下,按照上述收费标准,假设这批车需要![]() (
(![]() )年才能开始盈利,求
)年才能开始盈利,求![]() 的值.
的值.
参考数据:
|
|
|
|
|
|
|
|
|
|
其中其中![]() ,
,![]() ,
,
参考公式:对于一组数据![]() ,
,![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计公式分别为:
的斜率和截距的最小二乘估计公式分别为: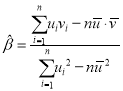 ,
,![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com