【题目】已知数列{an}的前n项和Sn＝－
n2＋
n，求数列{|an|}的前n项和Tn.
【答案】
【解析】试题分析：由Sn＝－
n2＋
n可得
，故可得当当n≤34时，an>0；当n≥35时，an<0，分两种情况求数列{|an|}的前n项和Tn
试题解析：
当n≥2时， 
，
an＝Sn－Sn－1＝－3n＋104.
又
时，a1＝S1＝－
×12＋
×1＝101，满足上式，
∴数列{an}的通项公式为an＝－3n＋104(n∈N*)．
由an＝－3n＋104≥0，得n≤34.7.
即当n≤34时，an>0；当n≥35时，an<0
①当n≤34时，
Tn＝|a1|＋|a2|＋…＋|an|
＝a1＋a2＋…＋an
＝Sn＝－n2＋n.
②当n≥35时，
Tn＝|a1|＋|a2|＋…＋|a34|＋|a35|＋…＋|an|
＝(a1＋a2＋…＋a34)－(a35＋a36＋…＋an)
＝2(a1＋a2＋…＋a34)－(a1＋a2＋…＋an)
＝2S34－Sn
＝2
－
＝n2－n＋3502.
综上Tn＝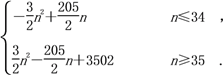
黎明文化寒假作业系列答案
寒假天地重庆出版社系列答案科目：高中数学 来源： 题型：
【题目】已知函数f（x）=x2﹣ax﹣2a2（x∈R）．
（1）关于x的不等式f（x）＜0的解集为A，且A[﹣1，2]，求a的取值范围；
（2）是否存在实数a，使得当x∈R时， 
成立．若存在给出证明，若不存在说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某单位附近只有甲、乙两个临时停车场，它们各有
个车位，为了方便市民停车，某互联网停车公司对这两个停车场，在某些固定时刻的剩余停车位进行记录，如下表：
时间 停车场 |
|
|
|
|
|
|
甲停车场 |
|
|
|
|
|
|
乙停车场 |
|
|
|
|
|
|
如果表中某一时刻剩余停车位数低于该停车场总车位数的
，那么当车主驱车抵达单位附近时，该公司将会向车主发出停车场饱和警报.
（1）假设某车主在以上六个时刻抵达单位附近的可能性相同，求他收到甲停车场饱和警报的概率；
（2）从这六个时刻中任选一个时刻,求甲停车场比乙停车场剩余车位数少的概率；
（3）当乙停车场发出饱和警报时，求甲停车场也发出饱和警报的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】设集合A={x|x2﹣3x+2=0}，B={x|x2+2（a+1）x+（a2﹣5）=0}．
（1）若A∩B={2}，求实数a的值；
（2）若A∪B=A，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
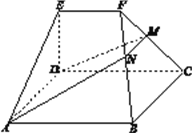
【题目】如图，在几何体
中，底面
为矩形， 
， 
．点
在棱
上，平面
与棱
交于点
．
（Ⅰ）求证： 
；
（Ⅱ）求证：平面
平面
；
（Ⅲ）若
， 
， 
，平面
平面
，求二面角
的大小．
查看答案和解析>>
科目：高中数学 来源： 题型：
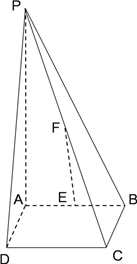
【题目】如图，四棱锥
的底面是边长为
的正方形， 
底面
， 
分别为
的中点.
（Ⅰ）求证： 
平面
；
（Ⅱ）若
，试问在线段
上是否存在点
，使得二面角 
的余弦值为
？若存在，确定点
的位置；若不存在，请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
