
【题目】已知函数![]() 为定义在
为定义在![]() 上的偶函数,当
上的偶函数,当![]() 时,
时,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(2)若函数![]() 有两个零点:求实数
有两个零点:求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的单调递减区间为
的单调递减区间为![]() ,
,![]() ,单调递增区间为
,单调递增区间为![]() ;(2)
;(2)![]() 或
或![]()
【解析】
![]() 根据题意求出函数
根据题意求出函数![]() 在
在![]() 上的单调区间,再利用偶函数在对称区间上单调性相反求出函数
上的单调区间,再利用偶函数在对称区间上单调性相反求出函数![]() 在区间
在区间![]() 上的单调区间即可;
上的单调区间即可;
![]() 由函数
由函数![]() 为定义在
为定义在![]() 上的偶函数,只需方程
上的偶函数,只需方程![]() 在
在![]() 上有一个根即可,分三种情况
上有一个根即可,分三种情况![]() ,
,![]() ,
,![]() 分别求出
分别求出![]() 时,函数
时,函数![]() 的解析式,利用函数的单调性求出其值域,进而求出实数
的解析式,利用函数的单调性求出其值域,进而求出实数![]() 的取值范围即可.
的取值范围即可.
(1)由题意可得,当![]() ,
,![]() 时,
时,![]() ,
,
令![]() ,即
,即![]() ,解得
,解得![]() ,
,
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
因为函数![]() 在
在![]() 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,所以
,所以![]() ,
,
因为函数![]() 在
在![]() 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
所以函数![]() 在
在![]() 上单调递增;
上单调递增;
因为函数![]() 为定义在
为定义在![]() 上的偶函数,
上的偶函数,
由偶函数在对称区间上单调性相反可得,
函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故函数![]() 单调递减区间为
单调递减区间为![]() ,
,![]() ,单调递增区间为
,单调递增区间为![]() .
.
(2)由题可得,函数![]() 有两个零点,
有两个零点,
即方程![]() 有两个不同根,
有两个不同根,
因为![]() 为定义在
为定义在![]() 上的偶函数,其图象关于
上的偶函数,其图象关于![]() 轴对称,
轴对称,
故方程![]() 在
在![]() 上有一个根即可.
上有一个根即可.
当![]() 时,则
时,则![]() ,因为
,因为![]() ,
,
所以当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上有一个根,
上有一个根,
由于![]() 在
在![]() 上单调递减,
上单调递减,![]() ,
,
所以![]() ,即
,即![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() ;
;
当![]() 时,令
时,令![]() ,解得
,解得![]() ,
,
因为函数![]() 为
为![]() 上的减函数,
上的减函数,
所以当![]() 时,
时,![]() ,
,
所以函数![]() 为
为![]() 上的减函数,
上的减函数,
所以![]() ,
,
当![]() 时,
时,![]() ,
,
所以函数![]() 为
为![]() 上的增函数,
上的增函数,
所以![]() ,
,
要使方程![]() 在
在![]() 上有一个根,
上有一个根,
只需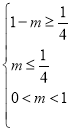 或
或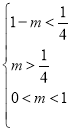 ,解得
,解得![]() 或
或![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() 或
或![]() ;
;
当![]() ,
,![]() 时,因为
时,因为![]() ,所以
,所以![]() ,
,
所以函数![]() ,
,
因为函数![]() 在
在![]() 上单调递减,
上单调递减,
所以函数![]() 在
在![]() 上单调递增,
上单调递增,
因为![]() ,所以
,所以![]() ,
,
即![]() ,
,
故只需![]() ,即
,即![]() ,
,
故实数![]() 的取值范围为
的取值范围为![]() .
.
综上可得,实数![]() 的取值范围为
的取值范围为![]() 或
或![]() .
.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:高中数学 来源: 题型:
【题目】某同学在一山坡![]() 处看对面山顶上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线
处看对面山顶上的一座铁塔,如图所示,塔及所在的山崖可视为图中的竖线![]() ,塔高
,塔高![]() 为80米,山高
为80米,山高![]() 为220米,
为220米,![]() 为200米,图中所示的山坡可视为直线
为200米,图中所示的山坡可视为直线![]() 且点
且点![]() 在直线
在直线![]() 上,
上,![]() 与水平地面的夹角为
与水平地面的夹角为![]() ,
,![]() .
.

(1)求塔尖![]() 到山坡的距离;(精确到米)
到山坡的距离;(精确到米)
(2)问此同学(忽略身高)距离山崖的水平地面多高时,观看塔的视角![]() 最大?
最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,直线
中,直线![]() 经过点
经过点![]() ,其倾斜角为
,其倾斜角为![]() ,以原点
,以原点![]() 为极点,以
为极点,以![]() 轴为非负半轴为极轴,与坐标系
轴为非负半轴为极轴,与坐标系![]() 取相同的长度单位,建立极坐标系.设曲线
取相同的长度单位,建立极坐标系.设曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)若直线![]() 与曲线
与曲线![]() 有公共点,求倾斜角
有公共点,求倾斜角![]() 的取值范围;
的取值范围;
(2)设![]() 为曲线
为曲线![]() 上任意一点,求
上任意一点,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】武汉有“九省通衢”之称,也称为“江城”,是国家历史文化名城.其中著名的景点有黄鹤楼、户部巷、东湖风景区等等.
(1)为了解“五·一”劳动节当日江城某旅游景点游客年龄的分布情况,从年龄在22岁到52岁的游客中随机抽取了1000人,制成了如图的频率分布直方图:
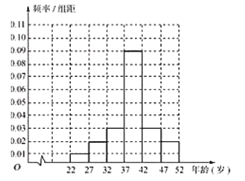
现从年龄在![]() 内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在
内的游客中,采用分层抽样的方法抽取10人,再从抽取的10人中随机抽取4人,记4人中年龄在![]() 内的人数为
内的人数为![]() ,求
,求![]() ;
;
(2)为了给游客提供更舒适的旅游体验,该旅游景点游船中心计划在2020年劳动节当日投入至少1艘至多3艘![]() 型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量
型游船供游客乘坐观光.由2010到2019这10年间的数据资料显示每年劳动节当日客流量![]() (单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
(单位:万人)都大于1.将每年劳动节当日客流量数据分成3个区间整理得表:
劳动节当日客流量 |
|
|
|
频数(年) | 2 | 4 | 4 |
以这10年的数据资料记录的3个区间客流量的频率作为每年客流量在该区间段发生的概率,且每年劳动节当日客流量相互独立.
该游船中心希望投入的![]() 型游船尽可能被充分利用,但每年劳动节当日
型游船尽可能被充分利用,但每年劳动节当日![]() 型游船最多使用量(单位:艘)要受当日客流量
型游船最多使用量(单位:艘)要受当日客流量![]() (单位:万人)的影响,其关联关系如下表:
(单位:万人)的影响,其关联关系如下表:
劳动节当日客流量 |
|
|
|
| 1 | 2 | 3 |
若某艘![]() 型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘
型游船在劳动节当日被投入且被使用,则游船中心当日可获得利润3万元;若某艘![]() 型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记
型游船劳动节当日被投入却不被使用,则游船中心当日亏损0.5万元.记![]() (单位:万元)表示该游船中心在劳动节当日获得的总利润,
(单位:万元)表示该游船中心在劳动节当日获得的总利润,![]() 的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘
的数学期望越大游船中心在劳动节当日获得的总利润越大,问该游船中心在2020年劳动节当日应投入多少艘![]() 型游船才能使其当日获得的总利润最大?
型游船才能使其当日获得的总利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 为奇函数,
为奇函数,![]() ,其中
,其中![]() .
.
(1)若函数![]() 的图像过点
的图像过点![]() ,求实数
,求实数![]() 和
和![]() 的值;
的值;
(2)若![]() ,试判断函数
,试判断函数![]() 在
在![]() 上的单调性并证明;
上的单调性并证明;
(3)设函数 ,若对每一个不小于3的实数
,若对每一个不小于3的实数![]() ,都恰有一个小于3的实数
,都恰有一个小于3的实数![]() ,使得
,使得![]() 成立,求实数
成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】数学中有许多形状优美、寓意美好的曲线,曲线C:![]() 就是其中之一(如图).给出下列三个结论:
就是其中之一(如图).给出下列三个结论:

①曲线C恰好经过6个整点(即横、纵坐标均为整数的点);
②曲线C上任意一点到原点的距离都不超过![]() ;
;
③曲线C所围成的“心形”区域的面积小于3.
其中,所有正确结论的序号是
A. ①B. ②C. ①②D. ①②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com