练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图，在三棱锥S﹣ABC中，G1 ， G2分别是△SAB和△SAC的重心，则直线G1G2与BC的位置关系是（ ）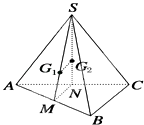

    A.相交
    B.平行
    C.异面
    D.以上都有可能

    【答案】B
    【解析】解：∵△SAB中，G1为的重心，
    ∴点G1在△SAB中线SM上，且满足SG1= SM
    同理可得：△SAC中，点G2在中线SN上，且满足SG2= SN
    ∴△SMN中， ，可得G1G2∥MN
    ∵MN是△ABC的中位线，∴MN∥BC
    因此可得G1G2∥BC，即直线G1G2与BC的位置关系是平行
    故选：B
    【考点精析】本题主要考查了空间中直线与直线之间的位置关系的相关知识点，需要掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点才能正确解答此题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知在△ABC中，角A，B，C的对边分别是a，b，c，向量m＝(2b，1)，n＝(2a－c，cos C)，且m∥n.(1)若b2＝ac，试判断△ABC的形状；(2)求y＝1－的值域．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，正确命题的个数是（ ）
    ①若2b=a+c，则a，b，c成等差数列；
    ②“a，b，c成等比数列”的充要条件是“b2=ac”；
    ③若数列{an2}是等比数列，则数列{an}也是等比数列；
    ④若| |=| |，则 = ．
    A.3
    B.2
    C.1
    D.0

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）= 为偶函数
    （1）求实数a的值；
    （2）记集合E={y|y=f（x），x∈{﹣1，1，2}}，λ=lg22+lg2lg5+lg5﹣ ，判断λ与E的关系；
    （3）当x∈[ ， ]（m＞0，n＞0）时，若函数f（x）的值域[2﹣3m，2﹣3n]，求实数m，n值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

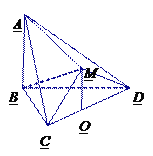
    【题目】如图，在多面体中，△是等边三角形，△是等腰直角三角形， ，平面 平面， 平面，点为的中点，连接.

    (1) 求证： ∥平面；

    (2)若，求三棱锥的体积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知实数a＞0， 方程 有且仅有两个不等实根，且较大的实根大于3，则实数a的取值范围 ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】2016年奥运会于8月5日在巴西里约热内卢举行，为了解某单位员工对奥运会的关注情况，对本单位部分员工进行了调查，得到平均每天看奥运会直播时间的茎叶图如下（单位：分钟），若平均每天看奥运会直播不低于70分钟的员工可以视为“关注奥运”，否则视为“不关注奥运”.

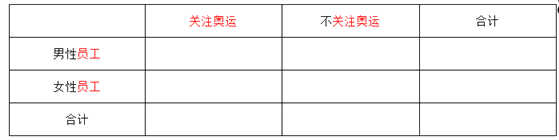
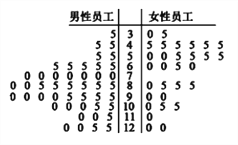
    （1）试完成下面表格，并根据此数据判断是否有99.5%以上的把握认为是否“关注奥运会”与性别有关？

    （2）若从参与调查且平均每天观看奥运会时间不低于110分钟的员工中抽取4人，用表示抽取的女员工数，求的分布列和期望值.

    参考公式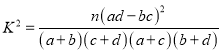： ，其中

    0.05

    0.025

    0.010

    0.005

    0.001

    3.841

    5.024

    6.635

    7.879

    10.828

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在如图所示的几何体中，四边形ABCD是等腰梯形，AB∥CD，∠DAB=60°，FC⊥平面ABCD，AE⊥BD，CB=CD=CF．
    （Ⅰ）求证：BD⊥平面AED；
    （Ⅱ）求二面角F﹣BD﹣C的余弦值．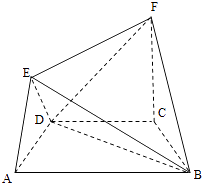

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，“嫦娥一号”探月卫星沿地月转移轨道飞向月球，在月球附近一点P变轨进入以月球球心F为一个焦点的椭圆轨道Ⅰ绕月飞行，之后卫星在P点第二次变轨进入仍以F为一个焦点的椭圆轨道Ⅱ绕月飞行，最终卫星在P点第三次变轨进入以F为圆心的圆形轨道Ⅲ绕月飞行，若用2c1和2c2分别表示椭圆轨道Ⅰ和Ⅱ的焦距，用2a1和2a2分别表示椭圆轨道Ⅰ和Ⅱ的长轴的长，给出下列式子：
    ①a1+c1=a2+c2；②a1﹣c1=a2﹣c2；③c1a2＞a1c2；④ ．
    其中正确式子的序号是（ ）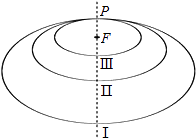

    A.①③
    B.②③
    C.①④
    D.②④

    查看答案和解析>>

    同步练习册答案