
分析 (1)设点M(x,y),$\overrightarrow{EF}=2\overrightarrow{EM}$则E(x,2y),代入抛物线y2=16x,即可得到轨迹方程.
(2)设过点(3,2)的直线为L:m(y-2)=x-3,直线L交于P、Q两点设点P(x1,y1),Q(x2,y2),联立直线L与曲线C,利用判别式以及韦达定理,求解kBP•kBQ.
解答 解:(1)设点M(x,y),$\overrightarrow{EF}=2\overrightarrow{EM}$则E(x,2y),
而动点E在抛物线y2=16x,
代入得C的方程为:y2=4x.…(4分)
(2)设过点(3,2)的直线为L:m(y-2)=x-3
直线L交于P、Q两点设点P(x1,y1),Q(x2,y2),直线L与曲线C
联立方程有:y2-4my+8m-12=0,
显然△>0.
∴y1+y2=4m,y1•y2=8m-12.…(6分)
∵${k_{BP}}•{k_{BQ}}=\frac{{{y_1}+2}}{{{x_1}-1}}•\frac{{{y_2}+2}}{{{x_2}-1}}=\frac{4}{{{y_1}-2}}•\frac{4}{{{y_2}-2}}=\frac{16}{{{y_1}{y_2}-2({{y_1}+{y_2}})+4}}$,…(10分)
即代入得kBP•kBQ=-2…(12分)
点评 本题考查轨迹方程的求法,直线与抛物线的位置关系的应用,考查计算能力.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:高中数学 来源: 题型:解答题
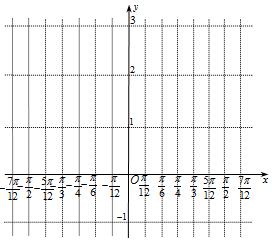 某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:
某同学用“五点法”画函数$f(x)=2sin(2x-\frac{π}{3})+1$在区间[-$\frac{π}{2}$,$\frac{π}{2}$]上的图象时,列表并填入了部分数据,如表:| 2x-$\frac{π}{3}$ | -$\frac{4π}{3}$ | -π | -$\frac{π}{2}$ | 0 | $\frac{π}{2}$ | $\frac{2π}{3}$ |
| x | -$\frac{π}{2}$ | -$\frac{π}{3}$ | -$\frac{π}{12}$ | $\frac{π}{6}$ | $\frac{5π}{12}$ | $\frac{π}{2}$ |
| f(x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
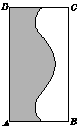 如图,面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为350个,试估计阴影部分的面积为( )
如图,面积为4的矩形ABCD中有一个阴影部分,若往矩形ABCD中随机投掷1000个点,落在矩形ABCD的非阴影部分中的点数为350个,试估计阴影部分的面积为( )| A. | 1.4 | B. | 1.6 | C. | 2.6 | D. | 2.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
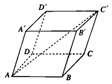 如图,在平行六面体ABCD-A'B'C'D'中,$AB=3,AD=4,AA'=4,∠BAD=\frac{π}{2}$,$∠BAA'=\frac{π}{3}$,$∠DAA'=\frac{π}{3}$,则AC'=$\sqrt{69}$.
如图,在平行六面体ABCD-A'B'C'D'中,$AB=3,AD=4,AA'=4,∠BAD=\frac{π}{2}$,$∠BAA'=\frac{π}{3}$,$∠DAA'=\frac{π}{3}$,则AC'=$\sqrt{69}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 14 | C. | 3 | D. | 21 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com