
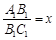 ,求公园ABCD所占面积S关于x的函数解析式;
,求公园ABCD所占面积S关于x的函数解析式;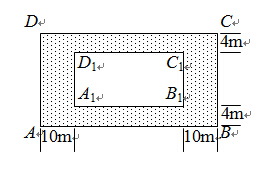
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案科目:高中数学 来源:不详 题型:解答题
 与时刻
与时刻 (时)的关系为
(时)的关系为 ,
,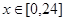 ,其中
,其中 是与气象有关的参数,且
是与气象有关的参数,且 ,用每天
,用每天 的最大值作为当天的污染指数,记作
的最大值作为当天的污染指数,记作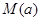 .
. ,
,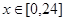 ,求
,求 的取值范围;
的取值范围;查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,则认为这批产品中有
,则认为这批产品中有 件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
件次品。某企业的统计资料显示,产品中发生次品的概率p与日产量n满足
 ,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失
,有已知每生产一件正品可赢利a元,如果生产一件次品,非但不能赢利,还将损失 元(
元( ).
). 的最大值;
的最大值;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①② | B.④① | C.③④ | D.③① |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 满足2
满足2 +
+ ,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+,
,对x≠0恒成立,在数列{an}、{bn}中,a1=1,b1=1,对任意x∈N+, ,
, 。
。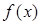 解析式;
解析式; ,总存在自然数k,当n≥k时,
,总存在自然数k,当n≥k时, 恒成立,求k的最小值。
恒成立,求k的最小值。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是定义在
是定义在 上的函数,且
上的函数,且 ,对任意
,对任意 ,若经过点
,若经过点 ,
, 的直线与
的直线与 轴的交点为
轴的交点为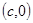 ,则称
,则称 为
为 关于函数
关于函数 的平均数,记为
的平均数,记为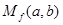 ,例如,当
,例如,当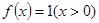 时,可得
时,可得 ,即
,即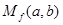 为
为 的算术平均数.
的算术平均数. 时,
时,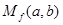 为
为 的几何平均数;
的几何平均数; 时,
时,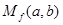 为
为 的调和平均数
的调和平均数 ;
;查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com