
【题目】已知函数f(x)的定义域为(﹣2,2),函数g(x)=f(x﹣1)+f(3﹣2x).
(1)求函数g(x)的定义域;
(2)若f(x)是奇函数且在定义域内单调递减,求不等式g(x)≤0的解集
【答案】
(1)解:∵数f(x)的定义域为(﹣2,2),函数g(x)=f(x﹣1)+f(3﹣2x).
∴ ,∴ <x< ,函数g(x)的定义域( , ).
(2)解:∵f(x)是奇函数且在定义域内单调递减,不等式g(x)≤0,
∴f(x﹣1)≤﹣f(3﹣2x)=f(2x﹣3),∴ ,
∴ <x<2,
不等式g(x)≤0的解集是 ( ,2).
【解析】分析:(1)由题意知, ![]() ,解此不等式组得出函数g(x)的定义域.(2)等式g(x)≤0,即 f(x﹣1)≤﹣f(3﹣2x)=f(2x﹣3),有
,解此不等式组得出函数g(x)的定义域.(2)等式g(x)≤0,即 f(x﹣1)≤﹣f(3﹣2x)=f(2x﹣3),有 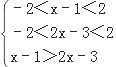 ,解此不等式组,可得结果.
,解此不等式组,可得结果.
【考点精析】解答此题的关键在于理解函数奇偶性的性质的相关知识,掌握在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.


科目:高中数学 来源: 题型:
【题目】某池塘中原有一块浮草,浮草蔓延后的面积y(m2)与时间t(月)之间的函数关系是y=at﹣1(a>0,且a≠1),它的图象如图所示.给出以下命题: ①池塘中原有浮草的面积是0.5m2;
②到第7个月浮草的面积一定能超过60m2
③浮草每月增加的面积都相等;
④若浮草面积达到4m2 , 16m2 , 64m2所经过时间分别为t1 , t2 , t3 , 则t1+t2<t3 , 其中所有正确命题的序号是( )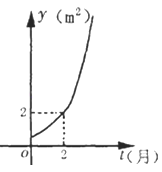
A.①②
B.①④
C.②③
D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设不等式-2<|x-1|-|x+2|<0的解集为M ,a,b∈M .
(Ⅰ)证明:|![]() |<
|<![]() ;
;
(Ⅱ)比较|1-4ab|与2|a-b|的大小,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+![]() +alnx.
+alnx.
(Ⅰ)若f(x)在区间[2,3]上单调递增,求实数a的取值范围;
(Ⅱ)设f(x)的导数f’(x )的图象为曲线C ,曲线C 上的不同两点A (x1, y1) ,B (x2,y 2) 所在直线的斜率为k ,求证:当a≤4时,|k|>1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】动点A(x , y)在圆x2+y2=1上绕坐标原点沿逆时针方向匀速旋转,12秒旋转一周.已知时间t=0时,点A的坐标是 ![]() ,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
,则当0≤t≤12时,动点A的纵坐标y关于t(单位:秒)的函数的单调递增区间是( )
A.[0,1]
B.[1,7]
C.[7,12]
D.[0,1]和[7,12]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床每天的租金)不超过10元时,床位可以全部租出,当床价高于10元时,每提高1元,将有3张床位空闲.为了获得较好的效益,该宾馆要给床位定一个合适的价格,条件是:①要方便结账,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.若用x表示床价,用y表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入).
(1)把y表示成x的函数,并求出其定义域;
(2)试确定该宾馆将床位定价为多少时,既符合上面的两个条件,又能使净收入最多?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列两个变量之间的关系哪个不是函数关系( )
A.角度和它的正切值
B.人的右手一柞长和身高
C.正方体的棱长和表面积
D.真空中自由落体运动物体的下落距离和下落时间
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com