
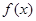 是定义在
是定义在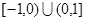 上的偶函数,当
上的偶函数,当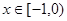 时,
时,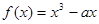 (
(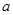 是实数)。
是实数)。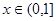 时,求f(x)的解析式;
时,求f(x)的解析式;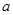 的取值范围;
的取值范围;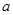 ,使得当
,使得当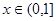 时,f(x)有最大值1.
时,f(x)有最大值1.
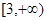
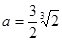 使得当
使得当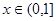 时,f(x)有最大值1
时,f(x)有最大值1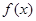 是定义在
是定义在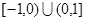 上的偶函数,当
上的偶函数,当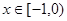 时的解析式,利用偶函数的的对称性得到结论。
时的解析式,利用偶函数的的对称性得到结论。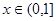 时,
时,
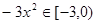 因为f(x)在(0,1]上是增函数,所以
因为f(x)在(0,1]上是增函数,所以
 则
则 ---------1分
---------1分 -------2分
-------2分 ---------4分
---------4分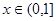 时,
时,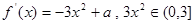
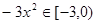
 -------------6分
-------------6分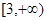 ---------7分
---------7分 时,由(2)知f(x)在区间(0,1]上是增函数
时,由(2)知f(x)在区间(0,1]上是增函数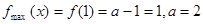 不合题意,舍去
不合题意,舍去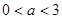 时,在区间(0,1]上,
时,在区间(0,1]上,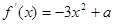
 -------------8分
-------------8分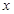 |  | 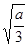 | 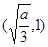 |
 | + | 0 | - |
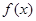 | 增 | 极大值 | 减 |
 处取得最大值 ----------9分
处取得最大值 ----------9分 -------------10分
-------------10分 --------11分
--------11分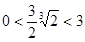 ,所以
,所以 符合题意 --------12分
符合题意 --------12分 时,在区间(0,1]上,
时,在区间(0,1]上, ,
,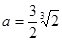 使得当
使得当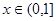 时,f(x)有最大值1、
时,f(x)有最大值1、

 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:不详 题型:解答题
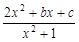 (b<0)的值域是[1,3],
(b<0)的值域是[1,3],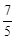 ≤F(|t-
≤F(|t-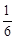 |-|t+
|-|t+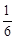 |)≤lg
|)≤lg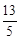 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 )=f(x)-f(y).
)=f(x)-f(y). )<2.
)<2.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com