
 若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )
若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )



 解:画出已知约束条件的可行域为△ABC内部(包括边界),
解:画出已知约束条件的可行域为△ABC内部(包括边界),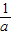 x+
x+ ,
,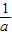 <0,故a>
<0,故a> .
. .
.

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案科目:高中数学 来源:2013年天津市耀华中学高考数学一模试卷(文科)(解析版) 题型:选择题
 若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )
若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )



查看答案和解析>>
科目:高中数学 来源:2011-2012学年北京市东城区示范校高三(下)3月联考数学试卷(理科)(解析版) 题型:选择题
 若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )
若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )



查看答案和解析>>
科目:高中数学 来源:2011年高考数学复习:6.3 三元一次不等式(组)与简单的线性规划问题(2)(解析版) 题型:选择题
 若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )
若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为( )



查看答案和解析>>
科目:高中数学 来源: 题型:
已知约束条件 若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为 ( )
若目标函数z=x+ay(a≥0)恰好在点(2,2)处取得最大值,则a的取值范围为 ( )
A.0<a< B.a≥ C.a> D.0<a<
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com