练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．函数y=ln（x2-4x+3）的单调减区间为（　　）
    A．（2，+∞）B．（3，+∞）C．（-∞，2）D．（-∞，1）

    分析 令t=x2-4x+3＞0，求得函数的定义域，且y=lnt，本题即求函数t在定义域上的减区间，再利用二次函数的性质得出结论．

    解答 解：令t=x2-4x+3＞0，求得x＜1，或x＞3，故函数的定义域为{x|x＜1，或x＞3}，且y=lnt．
    故本题即求函数t在定义域{x|x＜1，或x＞3}上的减区间．
    再利用二次函数的性质求得t在定义域{x|x＜1，或x＞3}上的减区间为（-∞，1），
    故选：D．

    点评 本题主要考查对数函数、二次函数的性质，复合函数的单调性，体现了转化的数学思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

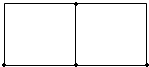    9．某自来水厂拟建一座平面图为矩形且面积为200m2的二级净水处理池（如图）．池的深度一定，池的外围周壁建造单价为400元/m，中间的一条隔壁建造单价为100元/m，池底建造单价为60元/m2，池壁厚度忽略不计．问净水池的长为多少时，可使总造价最低？

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知集合A={x|ax2-x+a+2=0，a∈R}．
    （1）若A中只有一个元素，求a的值，并把这个元素写出来；
    （2）若A中至多只有一个元素，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．函数f（x）=（a2-3a+3）logax是对数函数，则a的值是（　　）
    A．a=1或a=2B．a=1C．a=2D．a＞0或a≠1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知f（x）是定义在R上的奇函数，且当x＞0时，f（x）=ax-2其中a＞0且a≠1．
    （1）求f（2）+f（-2）的值；
    （2）求f（x）的解析式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．下列函数中，既是奇函数，又在（-∞，0）上单调递增的是（　　）
    A．y=x-1B．y=x2C．y=x3D．$y={x^{-\frac{1}{2}}}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=x2-ax+2a-3
    （1）若函数g（x）=f（6x）在（-∞，1）有两个不相等的零点，求a的取值范围；
    （2）若a=2，且存在实数t，当x∈[1，m]（m＞1）时，f（x+t）≤4x恒成立，求实数m的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    8．函数f（x）=2-x-1的定义域、值域是（　　）
    A．定义域是R，值域是RB．定义域是R，值域为（0，+∞）
    C．定义域是（0，+∞），值域为RD．定义域是R，值域是（-1，+∞）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．动圆M与定圆C1：x2+y2+6x=0外切，且内切于定圆C2：x2+y2-6x=40，求动圆圆心M的轨迹方程．

    查看答案和解析>>

    同步练习册答案