
【题目】已知函数![]() ,
,![]() (
(![]() ).
).
(Ⅰ)求![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)设![]() ,且
,且![]() 有两个极值点
有两个极值点![]() ,
,![]() ,其中
,其中![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(Ⅰ)见解析;(Ⅱ)![]()
【解析】
试题
本题考查利导数在研究函数问题中的应用。(Ⅰ)由题意得![]() ,根据函数
,根据函数![]() 图象的特点分
图象的特点分![]() 和
和![]() 两种情况讨论
两种情况讨论![]() 的符号,从而确定函数的单调增区间。(Ⅱ)由条件得
的符号,从而确定函数的单调增区间。(Ⅱ)由条件得![]() (
(![]() ),故可将问题转化为
),故可将问题转化为![]() ,
,![]() 是方程
是方程![]() 的两根的问题处理,然后根据
的两根的问题处理,然后根据![]() ,
,![]() 的关系可得
的关系可得![]()
![]() ,构造函数
,构造函数![]() ,
,![]() ,求其最小值即可。
,求其最小值即可。
试题解析:
(Ⅰ)由题意得![]() ,
,![]() ,
,
∴ ![]() ,
,
令![]() ,则其图象的对称轴为
,则其图象的对称轴为![]()
①当![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() ,得
,得![]() ,
,![]() ,
,
由![]() ,解得
,解得![]() 或
或![]() ,
,
∴![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]()
综上所述,当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]()
当![]() 时,
时,![]() 的单调递增区间为
的单调递增区间为![]() ,
,![]()
(Ⅱ)由题意得![]() ,(
,(![]() )
)
∴ ![]() (
(![]() ),
),
∵![]() 有两个极值点
有两个极值点![]() ,
,![]() ,
,
∴![]() ,
,![]() 是方程
是方程![]() 的两根,
的两根,
∴![]() ,
,![]() ,
,
∴ ![]() ,
,![]() ,
,
![]()
![]()
令![]() ,
,![]()
则![]()
![]()
当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递减,
上单调递减,
∴ ![]() 的最小值为
的最小值为![]() ,
,
即![]() 的最小值为
的最小值为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】经销商小王对其所经营的某一型号二手汽车的使用年数![]() 与销售价格
与销售价格![]() (单位:万元/辆)进行整理,得到如下的对应数据:
(单位:万元/辆)进行整理,得到如下的对应数据:
使用年数 | 2 | 4 | 6 | 8 | 10 |
售价 | 16 | 13 | 9.5 | 7 | 4.5 |
(1)试求![]() 关于
关于![]() 的回归直线方程;
的回归直线方程;
(2)已知每辆该型号汽车的收购价格为![]() 万元,根据(1)中所求的回归方程,预测
万元,根据(1)中所求的回归方程,预测![]() 为何值时,小王销售一辆该型号汽车所获得的利润
为何值时,小王销售一辆该型号汽车所获得的利润![]() 最大.
最大.
附:回归方程![]() 中,
中,
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极小值;
的极小值;
(2)设函数![]() ,试问:在定义域内是否存在三个不同的自变量
,试问:在定义域内是否存在三个不同的自变量![]() 使得
使得![]() 的值相等,若存在,请求出
的值相等,若存在,请求出![]() 的范围,若不存在,请说明理由?
的范围,若不存在,请说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下图是某地区2000年至2016年环境基础设施投资额![]() (单位:亿元)的折线图.
(单位:亿元)的折线图.
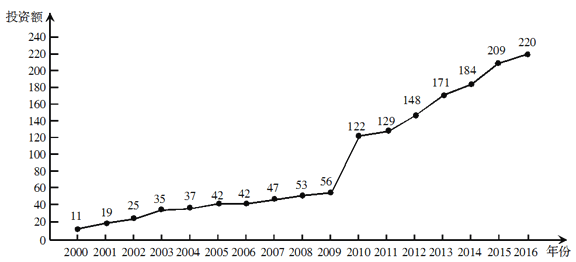
为了预测该地区2018年的环境基础设施投资额,建立了![]() 与时间变量
与时间变量![]() 的两个线性回归模型.根据2000年至2016年的数据(时间变量
的两个线性回归模型.根据2000年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型①:
)建立模型①:![]() ;根据2010年至2016年的数据(时间变量
;根据2010年至2016年的数据(时间变量![]() 的值依次为
的值依次为![]() )建立模型②:
)建立模型②:![]() .
.
(1)分别利用这两个模型,求该地区2018年的环境基础设施投资额的预测值;
(2)你认为用哪个模型得到的预测值更可靠?并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于![]() 的说法,正确的是( )
的说法,正确的是( )
A.展开式中的二项式系数之和为2048
B.展开式中只有第6项的二项式系数最大
C.展开式中第6项和第7项的二项式系数最大
D.展开式中第6项的系数最小
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,正四棱锥![]() 中,
中,![]() 为底面正方形的中心,侧棱
为底面正方形的中心,侧棱![]() 与底面
与底面![]() 所成的角的正切值为
所成的角的正切值为![]() .
.

(1)求侧面![]() 与底面
与底面![]() 所成的二面角的大小;
所成的二面角的大小;
(2)若![]() 是
是![]() 的中点,求异面直线
的中点,求异面直线![]() 与
与![]() 所成角的正切值;
所成角的正切值;
(3)问在棱![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() ⊥侧面
⊥侧面![]() ,若存在,试确定点
,若存在,试确定点![]() 的位置;若不存在,说明理由.
的位置;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,共享单车已经悄然进入了广大市民的日常生活,并慢慢改变了人们的出行方式.为了更好地服务民众,某共享单车公司在其官方![]() 中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出
中设置了用户评价反馈系统,以了解用户对车辆状况和优惠活动的评价.现从评价系统中选出![]() 条较为详细的评价信息进行统计,车辆状况的优惠活动评价的
条较为详细的评价信息进行统计,车辆状况的优惠活动评价的![]() 列联表如下:
列联表如下:
对优惠活动好评 | 对优惠活动不满意 | 合计 | |
对车辆状况好评 |
|
|
|
对车辆状况不满意 |
|
|
|
合计 |
|
|
|
(1)能否在犯错误的概率不超过![]() 的前提下认为优惠活动好评与车辆状况好评之间有关系?
的前提下认为优惠活动好评与车辆状况好评之间有关系?
(2)为了回馈用户,公司通过![]() 向用户随机派送每张面额为
向用户随机派送每张面额为![]() 元,
元,元,
![]() 元的 三种骑行券.用户每次使用
元的 三种骑行券.用户每次使用![]() 扫码用车后,都可获得一张骑行券.用户骑行一次获得
扫码用车后,都可获得一张骑行券.用户骑行一次获得![]() 元券,获得
元券,获得![]() 元券的概率分别是
元券的概率分别是![]() ,
,![]() ,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为
,且各次获取骑行券的结果相互独立.若某用户一天使用了两次该公司的共享单车,记该用户当天获得的骑行券面额之和为![]() ,求随机变量
,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以平面直角坐标系的原点O为极点,x轴的正半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位.曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标方程及曲线
的直角坐标方程及曲线![]() 的普通方程;
的普通方程;
(2)已知点![]() ,直线l的参数方程为
,直线l的参数方程为 (t为参数),设直线l与曲线
(t为参数),设直线l与曲线![]() 交于M,N两点,求
交于M,N两点,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com