
已知双曲线C的中心在原点,抛物线 的焦点是双曲线C的一个焦点,且双曲线经过点
的焦点是双曲线C的一个焦点,且双曲线经过点 ,又知直线
,又知直线 与双曲线C相交于A、B两点.
与双曲线C相交于A、B两点.
(1)求双曲线C的方程;
(2)若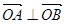 ,求实数k值.
,求实数k值.
(1)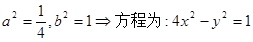 ;(2)
;(2)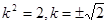 ,检验合格.
,检验合格.
解析试题分析:(1)先求抛物线的焦点为F( 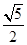 ,0),从而设双曲线方程,再将点(1,
,0),从而设双曲线方程,再将点(1, 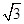 )代入,可求双曲线C的方程;(2)将直线方程与双曲线方程联立,将向量垂直条件转化为数量积为0,从而可得方程,进而可解.
)代入,可求双曲线C的方程;(2)将直线方程与双曲线方程联立,将向量垂直条件转化为数量积为0,从而可得方程,进而可解.
解:(1)抛物线的焦点是(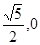 ),则双曲线的
),则双曲线的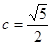 .………………1分
.………………1分
设双曲线方程: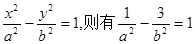 …………………………2分
…………………………2分
解得: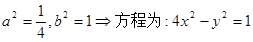 …………………………5分
…………………………5分
(2)联立方程:
当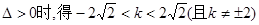 ……………………7分(未写△扣1分)
……………………7分(未写△扣1分)
由韦达定理: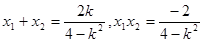 ……………………8分
……………………8分
设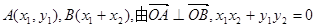
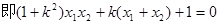 代入可得:
代入可得: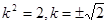 ,检验合格.……12分
,检验合格.……12分
考点:本题主要考查了以抛物线为载体,考查利用待定系数法求双曲线的标准方程,考查向量垂直。.
点评:解决该试题的关键是利用其数量积为0求解。同理能将抛物线的性质和双曲线的性质很好的结合起来求解双曲线的方程。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
(12分)已知椭圆 中心在原点,一个焦点为
中心在原点,一个焦点为 ,且长轴长与短轴长的比是
,且长轴长与短轴长的比是 。
。
(1)求椭圆 的方程;(5分)
的方程;(5分)
(2)是否存在斜率为 的直线
的直线 ,使直线
,使直线 与椭圆
与椭圆 有公共点,且原点
有公共点,且原点 与直线
与直线 的距离等于4;若存在,求出直线
的距离等于4;若存在,求出直线 的方程,若不存在,说明理由。(7分)。
的方程,若不存在,说明理由。(7分)。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)
在直角坐标系 中,点
中,点 到两点
到两点 ,
, 的距离之和等于
的距离之和等于 ,设点
,设点 的轨迹为
的轨迹为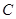 。
。
(1)求曲线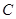 的方程;
的方程;
(2)过点 作两条互相垂直的直线
作两条互相垂直的直线 分别与曲线
分别与曲线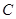 交于
交于 和
和 。
。
①以线段 为直径的圆过能否过坐标原点,若能求出此时的
为直径的圆过能否过坐标原点,若能求出此时的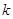 值,若不能说明理由;
值,若不能说明理由;
②求四边形 面积的取值范围。
面积的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分14分)
已知抛物线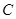 的顶点为坐标原点,焦点在
的顶点为坐标原点,焦点在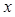 轴上. 且经过点
轴上. 且经过点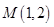 ,
,
(1)求抛物线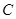 的方程;
的方程;
(2)若动直线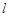 过点
过点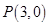 ,交抛物线
,交抛物线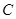 于
于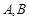 两点,是否存在垂直于
两点,是否存在垂直于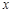 轴的直线
轴的直线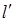 被以
被以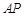 为直径的圆截得的弦长为定值?若存在,求出
为直径的圆截得的弦长为定值?若存在,求出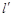 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题16分)在平面直角坐标系 中,
中,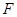 是抛物线
是抛物线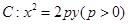 的焦点,
的焦点,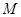 是抛物线
是抛物线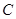 上位于第一象限内的任意一点,过
上位于第一象限内的任意一点,过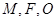 三点的圆的圆心为
三点的圆的圆心为 ,点
,点 到抛物线
到抛物线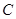 的准线的距离为
的准线的距离为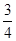 .
.
(Ⅰ)求抛物线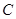 的方程;
的方程;
(Ⅱ)是否存在点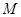 ,使得直线
,使得直线 与抛物线
与抛物线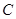 相切于点
相切于点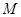 ?若存在,求出点
?若存在,求出点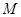 的坐标;若不存在,说明理由;
的坐标;若不存在,说明理由;
(Ⅲ)若点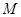 的横坐标为
的横坐标为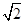 ,直线
,直线 与抛物线
与抛物线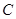 有两个不同的交点
有两个不同的交点 ,
,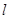 与圆
与圆 有两个不同的交点
有两个不同的交点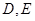 ,求当
,求当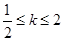 时,
时,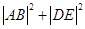 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)已知椭圆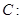
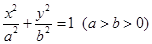 的离心率为
的离心率为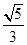 ,定点
,定点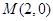 ,椭圆短轴的端点是
,椭圆短轴的端点是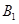 ,
, ,且
,且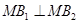 .
.
(1)求椭圆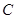 的方程;
的方程;
(2)设过点 且斜率不为
且斜率不为 的直线交椭圆
的直线交椭圆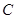 于
于 ,
, 两点.试问
两点.试问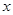 轴上是否存在定点
轴上是否存在定点 ,使
,使 平分
平分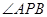 ?若存在,求出点
?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com