练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    当非零向量满足______________条件时，能使a+b平分a与b的夹角；满足______________条件时，能使|a+b|=|a-b|.

    解析：作=a,=b,以、为邻边作平行四边形，则a+b=,只有当OACB为菱形时，a+b才平分a与b的夹角.只有当平行四边形为矩形时，才能使其两条对角线相等，即|a+b|=|a-b|.

    答案：|a|=|b|  a⊥b

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    平面直角坐标系xOy中，已知A1（x1，y1），A2（x2，y2），…，An（xn，yn）是直线l：y=kx+b上的n个点
    （n∈N*，k、b均为非零常数）．
    （1）若数列{xn}成等差数列，求证：数列{yn}也成等差数列；
    （2）若点P是直线l上一点，且
    OP
    =a1
    OA1
    +a2
    OA2
    ，求a1+a2的值；
    （3）若点P满足
    OP
    =a1
    OA1
    +a2
    OA2
    +…+an
    OAn
    ，我们称
    OP
    是向量
    OA1
    ，
    OA2
    ，…，
    OAn
    的线性组合，{an}是该线性组合的系数数列．当
    OP
    是向量
    OA1
    ，
    OA2
    ，…，
    OAn
    的线性组合时，请参考以下线索：
    ①系数数列{an}需满足怎样的条件，点P会落在直线l上？
    ②若点P落在直线l上，系数数列{an}会满足怎样的结论？
    ③能否根据你给出的系数数列{an}满足的条件，确定在直线l上的点P的个数或坐标？
    试提出一个相关命题（或猜想）并开展研究，写出你的研究过程．[本小题将根据你提出的命题（或猜想）的完备程度和研究过程中体现的思维层次，给予不同的评分]．

    查看答案和解析>>

    科目：高中数学 来源：河南省郑州一中2007－2008年年上学期高三期中考试理科数学 题型：013

    已知非零向量，满足条件，向量，当实数t＝时，取最小值，则向量的夹角为

    [　　]

    A．60°

    B．45°

    C．30°

    D．150°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （本题满分20分，其中第1小题4分，第2小题6分，第3小题10分.）

    平面直角坐标系中，已知，…，是直线上的个点（，、均为非零常数）.

    （1）若数列成等差数列，求证：数列也成等差数列；

    （2）若点是直线上一点，且，求的值；

    （3）若点满足，我们称是向量，，…，的线性组合,是该线性组合的系数数列.

    当是向量，，…，的线性组合时，请参考以下线索：

    ① 系数数列需满足怎样的条件，点会落在直线上？

    ② 若点落在直线上，系数数列会满足怎样的结论？

    ③ 能否根据你给出的系数数列满足的条件，确定在直线上的点的个数或坐标？

    试提出一个相关命题（或猜想）并开展研究，写出你的研究过程.【本小题将根据你提出的命题（或猜想）的完备程度和研究过程中体现的思维层次，给予不同的评分】

    查看答案和解析>>

    科目：高中数学 来源：2011年上海市普陀区高考数学一模试卷（理科）（解析版） 题型：解答题

    平面直角坐标系xOy中，已知A1（x1，y1），A2（x2，y2），…，An（xn，yn）是直线l：y=kx+b上的n个点
    （n∈N*，k、b均为非零常数）．
    （1）若数列{xn}成等差数列，求证：数列{yn}也成等差数列；
    （2）若点P是直线l上一点，且，求a1+a2的值；
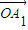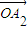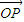    （3）若点P满足，我们称是向量，，…，的线性组合，{an}是该线性组合的系数数列．当是向量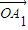，，…，的线性组合时，请参考以下线索：
    ①系数数列{an}需满足怎样的条件，点P会落在直线l上？
    ②若点P落在直线l上，系数数列{an}会满足怎样的结论？
    ③能否根据你给出的系数数列{an}满足的条件，确定在直线l上的点P的个数或坐标？
    试提出一个相关命题（或猜想）并开展研究，写出你的研究过程．[本小题将根据你提出的命题（或猜想）的完备程度和研究过程中体现的思维层次，给予不同的评分]．

    查看答案和解析>>

    同步练习册答案