
分析 先求出函数的导数,通过导函数,求解导函数值为负数时,求出函数的单调递减区间.
解答 解:函数y=-$\frac{2}{3}$x3+(a+$\frac{1}{a}$)x2-2x+4(a<-1)
可得y′=-2x2+2ax+$\frac{2}{a}$x-2=-2(x-a)(x-$\frac{1}{a}$),
令y′<0,得(x-a)(x-$\frac{1}{a}$)>0.
∵a<-1,∴a<-1$<\frac{1}{a}$<0,不等式解为x<a或x>$\frac{1}{a}$,
此时函数的单调递减区间为(a,$\frac{1}{a}$).
故答案为:(a,$\frac{1}{a}$).
点评 本题考查了函数的单调性,考查导数的应用,是一道中档题.


科目:高中数学 来源:2015-2016学年吉林省高一下学期期末联考数学试卷(解析版) 题型:选择题
不等式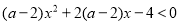 对一切
对一切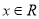 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A.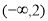 B.[-2,2] C.(-2,2] D.
B.[-2,2] C.(-2,2] D.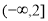
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 组别 | [65,75) | [75,85) | [85,95) | [95,105) | [105,115) | [115,150) |
| 频数 | 3 | 4 | 13 | 15 | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 都与直线a相交的两条直线确定一个平面 | |
| B. | 两条直线确定一个平面 | |
| C. | 过一条直线的平面有无数多个 | |
| D. | 两个相交平面的交线是一条线段 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com